The Pentagonal Bipyramid

---

The pentagonal bipyramid is a polyhedron bounded by 10 isosceles triangles, 15 edges, and 7 vertices. It is the dual of the pentagonal prism. It belongs to the class of duals of uniform polyhedra, which also includes the Catalan solids.

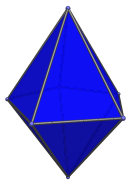
The faces are transitive isosceles triangles with 2 short edges and 1 long edge. The edge length ratio is 3−φ : 2, or approximately 0.691 : 1, where φ=(1+√5)/2 is the Golden Ratio.

Note that the pentagonal bipyramid as the dual of the (uniform) pentagonal prism should not be confused with Johnson solid J13, which is also a pentagonal bipyramid, but with regular faces—equilateral triangles rather than isosceles triangles. The dual of J13 is a non-uniform pentagonal prism, having rectangular rather than square faces, with edge length ratio is √(25−11√5) : √2, or approximately 0.449 : 1.

Projections

The following are images of the pentagonal bipyramid from various viewpoints:

Projection	Description
	Top view.
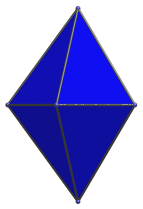
	Edge-centered side view.
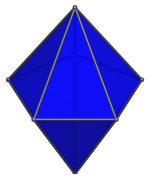
	Oblique side view.
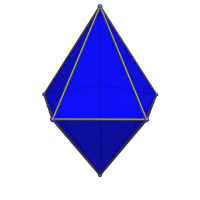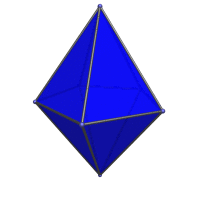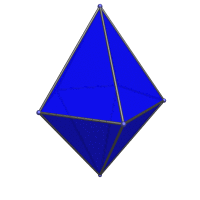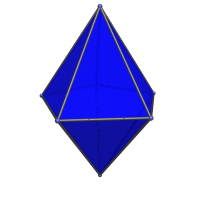
	Face-centered view.

Animation

Here's an animation of the pentagonal bipyramid rotating around its vertical axis:

Coordinates

The Cartesian coordinates for the pentagonal bipyramid are:

• (0, 0, ±(6φ+2)/5)
• (−√((10+2√5)/5), 0, 0)
• (−√((5−2√5)/10), ±φ, 0)
• (√((5+2√5)/5), ±1, 0)

These coordinates correspond with a dual pentagonal prism of edge length (3φ−4).