The Square Trapezohedron
The square trapezohedron is a polyhedron bounded by 8 kites, 16 edges (8 long, 8 short), and 10 vertices. It is the dual of the square antiprism. It belongs to the class of duals of uniform polyhedra, which also includes the Catalan solids.
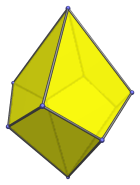
The faces are congruent kites with 2 short edges and 2 long edges, with an edge length ratio is (2−√2) : 1, or approximately 0.586 : 1. The ratio of short to long diagonal is √2 : √(1+2√2), or approximately 0.723 : 1.
Projections
The following are images of the square trapezohedron from various viewpoints:
| Projection | Description |
|---|---|
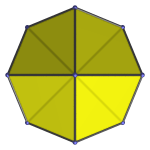 |
Top view. |
 |
Front view, looking at an equatorial vertex. |
 |
Oblique side view. |
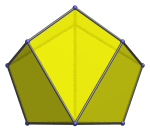 |
Apex view parallel to one face. |
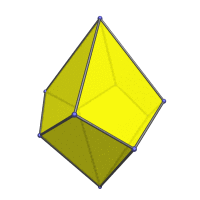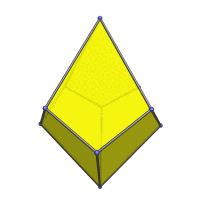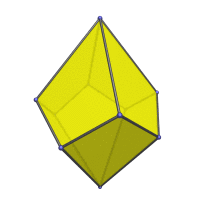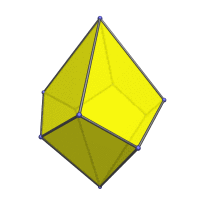
Animation
Here is an animation of the square trapezohedron rotating around its vertical axis:
Coordinates
The Cartesian coordinates for the square trapezohedron are:
- (0, 0, ±(∜2 + 1/∜2))
- (0, ±√2, ∜2 − 1/∜2)
- (±√2, 0, ∜2 − 1/∜2)
- (±1, ±1, −(∜2 − 1/∜2))
These coordinates are obtained by inverting a square antiprism of edge length (4−2√2).
Occurrences
The square trapezohedron occurs as cells in the square antitegmatic hecatontetracontatetrachoron, one of the Catalan polychora in the 24-cell family, albeit in slightly different proportions: having edge ratio 2√(5−3√2) : √7 (approx. 0.658 : 1), rather than (2−√2) : 1 (approx. 0.586 : 1).




