The Square Antitegmatic Hecatontetracontatetrachoron
The square antitegmatic hecatontetracontatetrachoron is a Catalan polychoron bounded by 144 square trapezohedra, 576 kites, 672 edges (288 short, 384 long), and 240 vertices. It is the dual of the runcinated 24-cell.

The cells are transitive, and are square trapezohedra with an edge length ratio of 2√(5−3√2) : √7, or approximately 0.658 : 1. The following image shows an individual cell:

The dual of this cell is a non-uniform square antiprism whose lacing edges (the edges linking its two square faces) are longer than the edges of its square faces by a factor of √2.
Structure
We will explore the structure of the square antitegmatic hecatontetracontatetrachoron using its parallel projections into 3D.
The First Layer
The following images show three pairs of square trapezohedral cells situated around the vertex that the 4D viewpoint is looking at.



The Second Layer
Surrounding these 6 cells are a layer of another 24 cells, each sharing a face with one of these cells. The following images incrementally show these cells, in groups of 8:



The Third Layer
Six more square trapezohedra fit into the bowl-shaped depressions, touching the vertices of the cells from the first layer:

The Fourth Layer
Straddling the shallow valleys between the 2nd layer cells are another 24 cells, shown next:


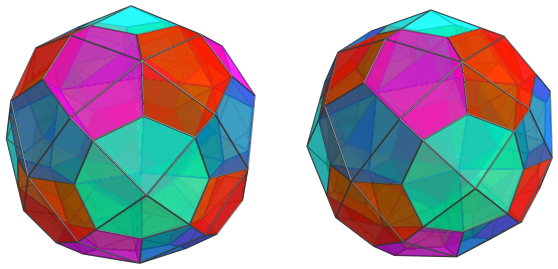
These are all the cells that lie on the near side of the polytope, its
northern hemisphere
. Following this, we come to the limb, or
equator
, of the polytope.
The Equator
There are 24 cells that lie on the limb of the polychoron, in 3 rings of 8 cells each, as shown below:
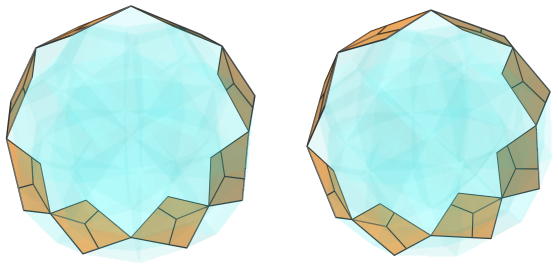

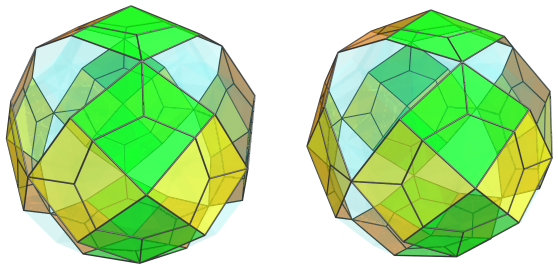
These cells lie at a 90° angle to the 4D viewpoint, and so appear to be flat. In 4D, of course, they are full-bodied square trapezohedra. For the sake of clarity, we have omitted the cells we saw earlier.
Past this point, the layers we have seen so far repeat in reverse order in
the southern hemisphere
of the polytope.
The remaining gaps in the equator do not correspond to any cells; they are where the 4th layer cells of the northern hemisphere touch the corresponding 4th layer cells in the southern hemiphere.
Summary
In summary, there are 6 cells in the first layer, 24 cells in the 2nd layer, 6 cells in the 3rd layer, and 24 cells in the 4th layer, for a total of 60 cells in the northern hemisphere. There are 24 cells in the equator, and another 60 cells in the southern hemisphere, for a grand total of 60 + 24 + 60 = 144 square trapezohedral cells.
Relation to Hopf Fibration
The cells in the square antitegmatic hecatontetracontatetrachoron can be partitioned into 3 sets of 48, each set consisting of six rings, each of which consists of 8 cells joined to each other by their apical vertices. Each set of rings represents a discrete subset of the Hopf fibration of the 3-sphere.
The following images show one such set of rings. The first image shows the first ring:

Apparently only 4 cells are shown here, but actually there are 8 cells: 4 cells on the far side of the polytope project to the same images as the 4 cells on the near side.
The next image shows the second ring:
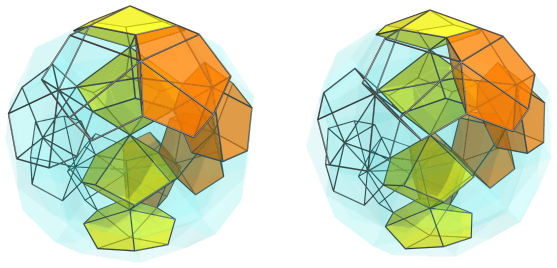
Four of the cells are shown here only in outline, because they lie on the far side of the polychoron.
The next image shows the 3rd ring, again with the far side cells only in outline:
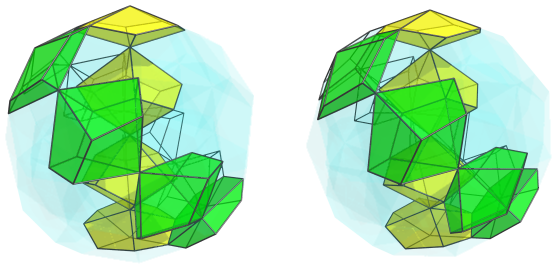
The following image shows the 4th ring:

And the 5th ring:

Finally, the last ring wraps around the equator:

Here are all the rings together:
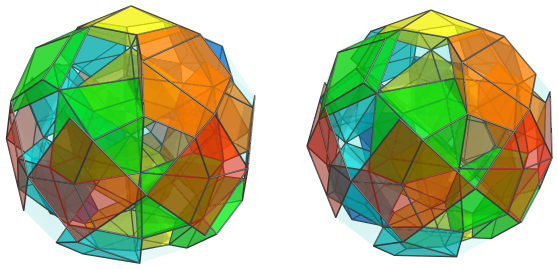
For the sake of clarity, we show only the cells on the near side of the polytope.
Coordinates
The Cartesian coordinates of the square antitegmatic hecatontetracontatetrachoron are all permutations of coordinate and changes of sign of:
- (0, 0, 0, 2)
- (0, 0, √2, √2)
- (0, 2√2−2, 2√2−2, 4√2−4)
- (0, 4−2√2, 4−2√2, 4−2√2)
- (2−√2, 2−√2, 2−√2, 6−3√2)
- (1, 1, 1, 1)
These coordinates correspond with a dual runcinated 24-cell of edge length (1−√2/2).




