The Joined Pentachoron

---

The joined pentachoron is a Catalan polychoron bounded by 10 triangular bipyramids, 30 isosceles triangles, 30 edges (10 long, 20 short), and 10 vertices. It is the dual of the rectified 5-cell.

The cells are triangular bipyramids with isosceles triangular faces with an edge length ratio of 2 : 2 : 3. They are duals of the uniform triangular prism.

The projection envelope of the joined pentachoron is a triakis tetrahedron, a Catalan solid.

Joined in the name refers to the join operator in Conway's polyhedron notation (suitably generalized to 4D), which can be applied to the 5-cell to obtain this polytope.

Structure

We will explore the structure of the joined pentachoron using its parallel projections into 3D.

The Near Side

The following images show the 4 cells facing the 4D viewpoint.

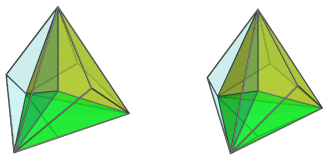
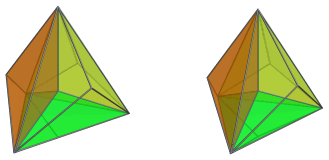
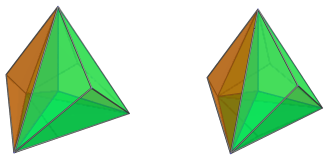
These cells look flatter than they are in 3D; this is because they lie at an angle to the 4D viewpoint and therefore have been foreshortened by the parallel projection.

All 4 cells share a common vertex in the middle of the projection, which is the closest vertex to the 4D viewpoint. It is where 4 apices of the cells meet. There are 5 such vertices in the joined pentachoron.

These are all the cells that lie on the near side of the polytope.

The Far Side

Following this, we come to the far side of the polytope. There are 6 cells here, as shown below in 3 pairs:

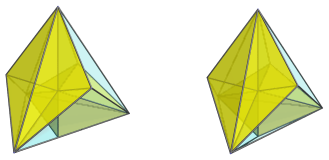
These cells appear distorted because of their oblique angle with the 4D viewpoint. However, this is merely an artifact of the parallel projection.

The vertex in the center of the projection is shared by all 6 cells, and is where these cells' equators meet. It is antipodal to the central point on the near side of the polytope. There are 5 such vertices in the joined pentachoron.

The following image shows all 6 far side cells together:

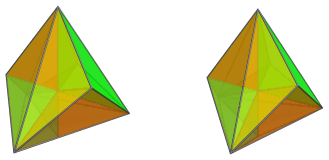
Summary

In summary, there are 4 cells on the near side of the polychoron and 6 cells on the far side, for a total of 10 cells.

Animation

Here's an animation of the joined pentachoron rotating in the WY plane:

Coordinates

The Cartesian coordinates of the joined pentachoron are:

• (−5/(6√10), −5/(6√6), −5/(6√3), ±5/6)
• (−5/(6√10), −5/(6√6), 5/(3√3), 0)
• (−5/(6√10), 5/(2√6), 0, 0)
• (5/(4√10), 5/(4√6), 5/(4√3), ±5/4)
• (5/(4√10), 5/(4√6), −5/(2√3), 0)
• (5/(4√10), −15/(4√6), 0, 0)
• (10/(3√10), 0, 0, 0)
• (−5/√10, 0, 0, 0)

These coordinates correspond with a dual rectified 5-cell of edge length 2.