The Triangular Antitegmatic Hexacontatetrachoron
The triangular antitegmatic hexacontatetrachoron is a Catalan polychoron bounded by 64 triangular trapezohedra, 192 kites (96 large, 96 small), 208 edges (64 short, 96 medium, 48 long), and 80 vertices. It is the dual of the runcinated tesseract.

As a Catalan polychoron, it is cell-transitive. Each cell is a triangular trapezohedron having triangular symmetry around its axis.
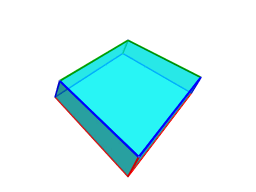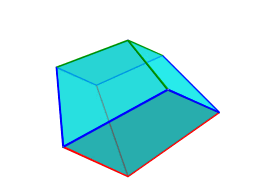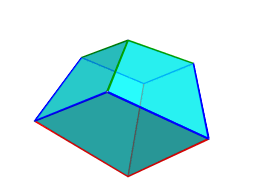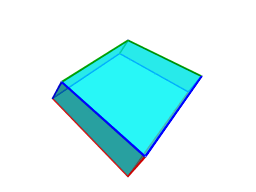
On one end of this axis is a cluster of 3 short edges, shown above in green,
and on the other end a cluster of 3 long edges, shown above in red. Wrapping
around its equator
are 6 medium length edges, shown above in blue. The
edge length ratio (short : medium : long) is (1/7)√(76+37√2) : 2 : 4−√2, or
approximately 0.809 : 1 : 1.293.
As can be seen above, the kite faces of each cell are of two kinds: small kites having two short edges and two medium edges, and large kites having two medium edges and two large edges. There are a total of 96 small kites and 96 large kites in the entire polytope.
The vertices are of 4 kinds: 8 corresponding with an embedded 16-cell, 24 corresponding with an embedded 24-cell (rectified 16-cell), 32 corresponding with a rectified tesseract, and 16 corresponding with an embedded tesseract, for a total of 80 vertices.
The projection envelope of the triangular antitegmatic hexacontatetrachoron is the deltoidal icositetrahedron (with exact proportions), the analogous Catalan solid.
Structure
We will explore the structure of the triangular antitegmatic hexacontatetrachoron using its parallel projections into 3D.


The above images show the 8 triangular trapezohedral cells touching the vertex that lies closest to the 4D viewpoint. For clarity, we render the other cells in a light transparent color.
Surrounding these cells are another 24 cells, shown below:



These cells look somewhat distorted because they lie at an angle to the 4D viewpoint and are foreshortened by the projection into 3D. In 4D, however, they are identical to the previous cells.
These are all the cells that lie on the near side of the polychoron. After this point, the same layout of cells repeat in reverse order on the far side of the polytope. Thus, on the near side there are 8 + 24 = 32 cells, and on the far side there are 24 + 8 = 32 cells, for a total of 64 cells.
Coordinates
The Cartesian coordinates of the triangular antitegmatic hexacontatetrachoron are all permutations of coordinate and changes of sign of:
- (0, 0, 0, 14(√2−1))
- (0, 0, 7(2−√2), 7(2−√2))
- (0, 2(3−√2), 2(3−√2), 2(3−√2))
- ((4−√2), (4−√2), (4−√2), (4−√2))
These coordinates correspond with a dual runcinated tesseract of edge length 1/7.




