The Runcinated 24-cell
The runcinated 24-cell is a uniform polychoron bounded by 240 cells (48 octahedra, 192 triangular prisms), 672 polygons (384 triangles, 288 squares), 576 edges, and 144 vertices. It may be constructed by expanding the 24 cells of a 24-cell outwards radially and filling in the resulting gaps with triangular prisms and 24 more octahedra.

The dual of the runcinated 24-cell is the square antitegmatic hecatontetracontatetrachoron, a Catalan polychoron.
Structure
We shall explore the structure of the runcinated 24-cell by means of its parallel projection into 3D, centered on an octahedral cell.
The Octahedra

The above image shows the nearest octahedral cell. Its 6 vertices are shared with 6 other octahedral cells, shown below:
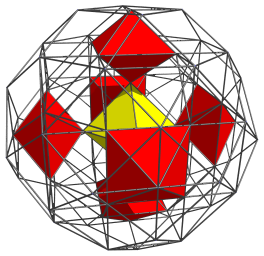
The 48 octahedra of the runcinated 24-cell correspond with two sets of 24 octahedra each: one corresponding with the cells of one 24-cell, and the other corresponding with the cells of the dual 24-cell. The nearest octahedron (yellow) corresponds with one of the cells of the first 24-cell, and the other 6 (red) with the cells of its dual. To emphasize this correspondence, we shall color all octahedra from the first 24-cell yellow, and all octahedra from the dual 24-cell red.
There are 8 more octahedra from the first set that share vertices with these red octahedra:
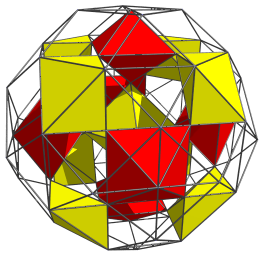
All 15 of these octahedra lie on the “northern hemisphere” of the runcinated 24-cell. At the equator there are 6 more octahedra of the first set:

And 12 more octahedra from the second set:

These octahedra appear as squares and rhombuses because they are being viewed from a 90° angle. They are regular octahedra in 4D.
This makes a total of 18 octahedra on the equator. Past this point, there are another 15 octahedra in the “southern hemisphere” of the runcinated 24-cell, in an arrangement that exactly mirrors the northern hemisphere octahedra. In total, this makes 15 + 18 + 15 = 48 octahedra.
The Triangular Prisms
Filling the gaps between the 48 octahedra that we have seen are 192 triangular prisms. We'll explore them using the same parallel projection, starting with the following 8 triangular prisms which share a face with the nearest octahedron:

Straddling these triangular prisms are another 12 triangular prisms:

Another 12 triangular prisms in complementary orientation lie over them:

Over these are another 24 triangular prisms, which close up the octahedral gaps filled by the 6 red octahedral cells we saw earlier:


Straddling these triangular prisms are another 24 that begin to close up the gaps occupied by the 8 yellow octahedral cells seen earlier:

These are all the triangular prisms in the northern hemisphere of the runcinated 24-cell. The 8 triangular gaps looking into the octahedral holes are filled in by 8 triangular prisms on the equator, foreshortened to triangles because they are viewed from a 90° angle:

To reduce clutter, we omit the other cells that we have seen so far, except for the nearest octahedron, left in for reference.
The edges of these 8 triangular images are actually foreshortened square faces of the triangular prisms. These square faces are joined to another 24 triangular prisms on the equator:

The remaining gaps on the equator are octahedral cells, as we have previously seen. We show all the equatorial cells together below:

In summary, we have 8+12+12+24+24=80 triangular prisms in the northern hemisphere of the runcinated 24-cell, and 8+24=32 triangular prisms on its equator. The southern hemisphere exactly mirrors the structure of the northern hemisphere (in reverse order), having another 80 triangular prisms. Thus, there is a total of 80+32+80=192 triangular prisms.
Perspective projection
The perspective projection of the runcinated 24-cell, centered on an octahedron, is shown below:

For clarity, we have omitted cells that lie on the far side of the runcinated 24-cell, including the equatorial cells because of the perspective projection.
Coordinates
The Cartesian coordinates of the runcinated 24-cell, centered on the origin and with edge length 2, are all permutations of coordinates and changes of sign of the following two points:
- (0, 0, √2, 2+√2)
- (1, 1, 1+√2, 1+√2)
Properties
The runcinated 24-cell has a higher degree of symmetry than the 24-cell, because its 48 octahedral cells correspond with both the vertices and cells of a 24-cell, and its 192 triangular prisms correspond with both the faces and edges of the 24-cell, making these two pairs of element types (cells/vertices and faces/edges) interchangeable, thus doubling the number of symmetries. A few other members of the 24-cell family of uniform polychora exhibit this extended symmetry, including the bitruncated 24-cell and the omnitruncated 24-cell.




