The Runcitruncated 120-cell

---

The runcitruncated 120-cell is a beautiful 4D polytope in the 120-cell/600-cell family of uniform polychora. Its surface consists of 2640 cells (120 truncated dodecahedra, 720 decagonal prisms, 1200 triangular prisms, 600 cuboctahedra), 13440 polygons (4800 triangles, 7200 squares, 1440 decagons), 18000 edges, and 7200 vertices.

Structure

First Layer

We will explore the structure of the runcitruncated 120-cell using its parallel projections into 3D, centered on a truncated dodecahedron.

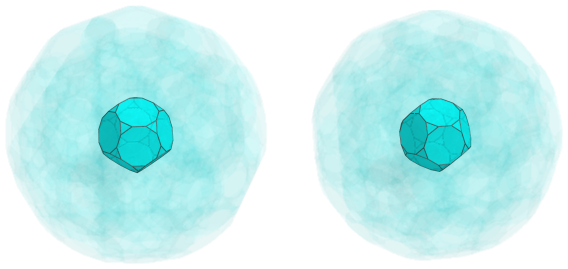
The above image shows the nearest cell to the 4D viewpoint: a truncated dodecahedron. For the sake of clarity, we have omitted the edges not lying on this cell, and have rendered all the other cells in a light transparent color.

Surrounding this cell are 12 decagonal prisms, touching its decagonal faces:

Straddling each pair of adjacent decagonal prisms are triangular prisms, 30 of them in total, which touch 30 of the edges of the truncated dodecahedron:

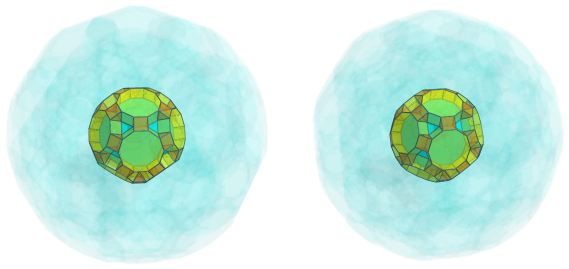
Twenty cuboctahedra touch its triangular faces, straddling the decagonal prisms:

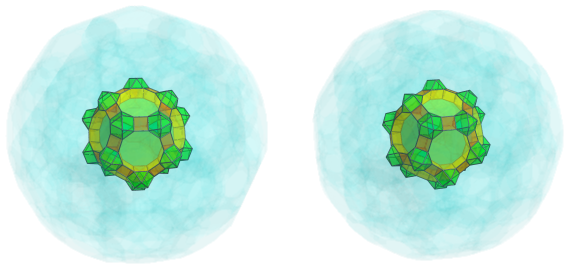
Second Layer

The cuboctahedra from the previous layer have 20 triangular prisms emanating from them:

On the other ends of these triangular prisms are 20 other cuboctahedra:

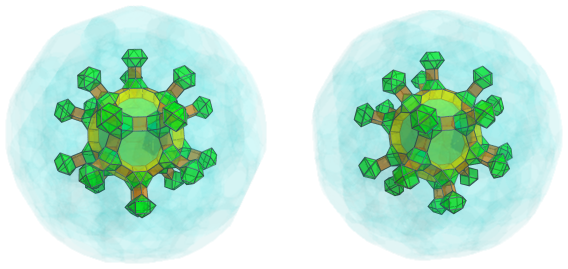
Between these protruding triangular prisms and cuboctahedra are 30 decagonal prisms:

The cup-shaped depressions are filled by twelve more truncated dodecahedra:

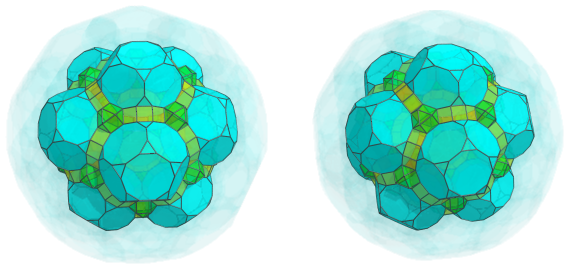
Third Layer

Surrounding the exposed cuboctahedra of the previous layer are more triangular prisms, 3 per cuboctahedron, for a total of 60 more triangular prisms:

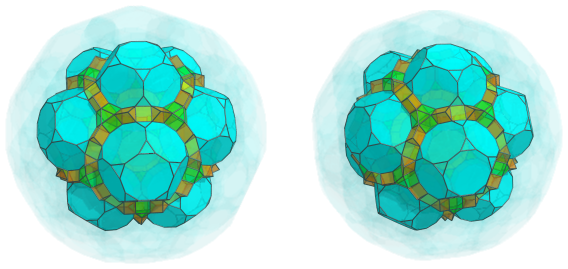
These triangular prisms converge on 30 more cuboctahedra, that sit between each pair of adjacent truncated dodecahedra:

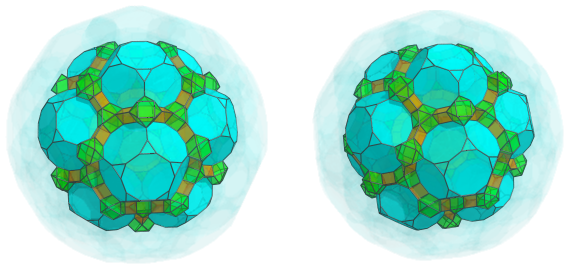
You can see the alternating bands of triangular prisms and cuboctahedra start to trace out outlines of decagonal prisms above the decagonal faces of the truncated dodecahedra. The following image shows the 60 decagonal prisms that fit in these outlines:

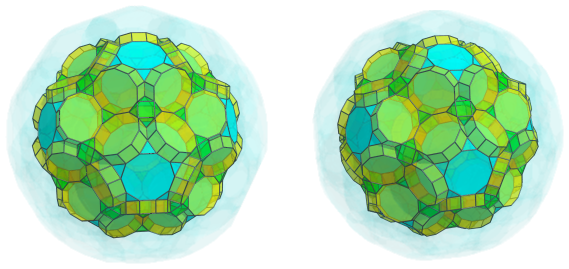
Another 60 triangular prisms fill in the little gaps between the cuboctahedra and truncated dodecahedra:

The other ends of these triangular prisms are joined to 60 more cuboctahedra:

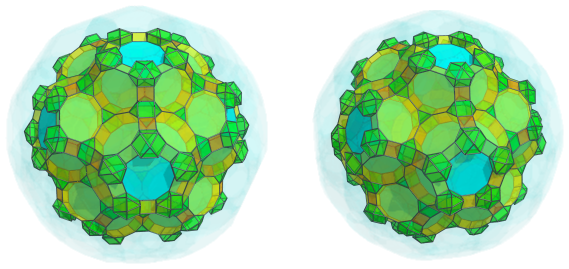
These cuboctahedra are linked by yet another 60 triangular prisms:

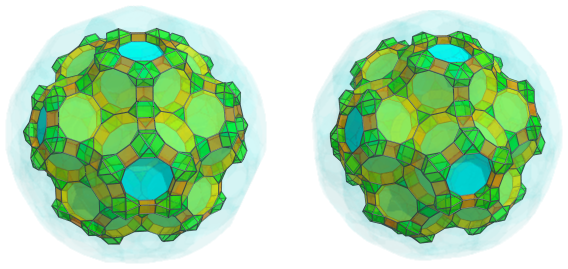
The obvious decagonal gaps encircled by these cells are filled in by 12 decagonal prisms, above the decagonal faces of the truncated dodecahedra:

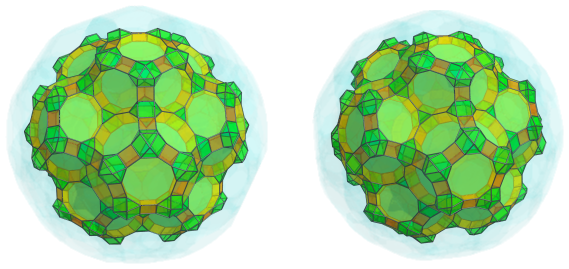
Finally, the cup-shaped depressions are filled by 20 more truncated dodecahedra:

Fourth Layer

The 20 truncated dodecahedra from the previous layer are linked to each other by 30 decagonal prisms:

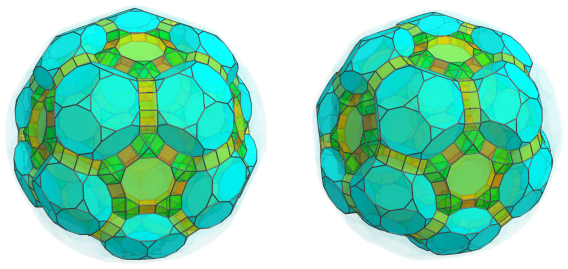
There are 60 triangular prisms sitting between these prisms and the adjacent cuboctahedra, continuing the pattern of alternating cuboctahedra and triangular prisms:

Another 60 cuboctahedra sit atop these triangular prisms:

Of course, they are linked by 30 triangular prisms:

This pattern of alternating cuboctahedra and triangular prisms will eventually encircle 60 more decagonal prisms. We show below the decagonal prisms fitted into the as-yet incomplete circles of alternating cuboctahedra and triangular prisms:

It should be obvious now that another 12 truncated dodecahedra fit into the cup-shaped depressions formed by these decagonal prisms:

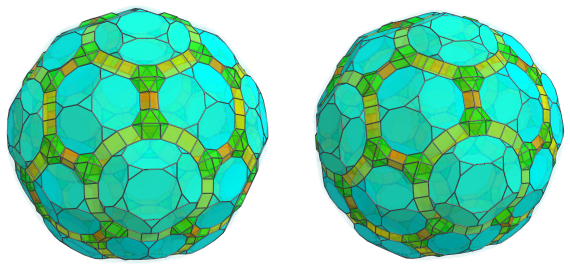
Fifth Layer

Continuing with the alternating cuboctahedra and triangular prisms, the next image shows 120 more triangular prisms emanating from the visible cuboctahedra:

And the 60 cuboctahedra that bridge them:

All the remaining exposed decagonal faces of the truncated dodecahedra are joined to decagonal prisms. Twelve of these decagonal prisms lie on the equator, which will be shown later; of the remaining, there are 3*20 + 5*12 = 120 decagonal prisms, shown next:

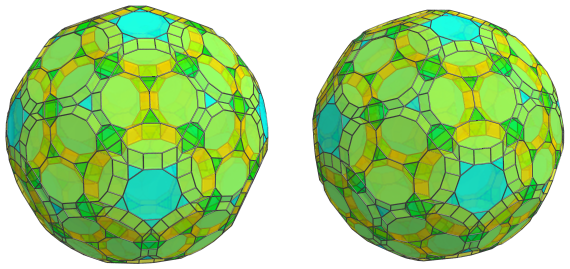
Straddling these prisms are another 120 triangular prisms, emanating from the 60 cuboctahedra:

Finally, these triangular prisms converge on 20 cuboctahedra:

These are all the cells that lie on the near side of the runcitruncated 120-cell.

The Equator

Now we come to the equator, or the limb, of the runcitruncated 120-cell. These are the cells that are oriented at a 90° angle to the 4D viewpoint.

First, we begin with the 30 truncated dodecahedra that lie on the equator:

For the sake of clarity, we have omitted the cells we have seen earlier. Due to the fact that these truncated dodecahedra are seen at a 90° angle from the 4D viewpoint, they appear foreshortened into flat, irregular decagons; but in reality, they are perfectly uniform truncated dodecahedra.

Just as with the truncated dodecahedra on the near side of the polytope, these cells are linked to each other by decagonal prisms, 60 in number:

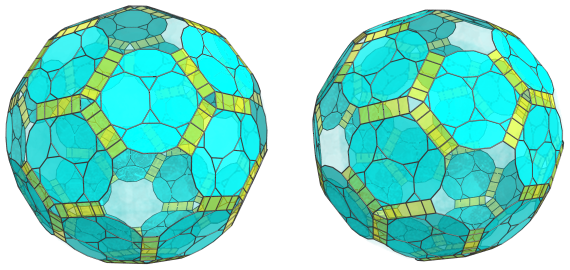
As with the truncated dodecahedra, these cells are seen from a 90° angle from the 4D viewpoint, so they appear foreshortened into rectangles. In 4D space, they are perfectly uniform decagonal prisms.

There are 20 triangular prisms sitting where these decagonal prisms meet:

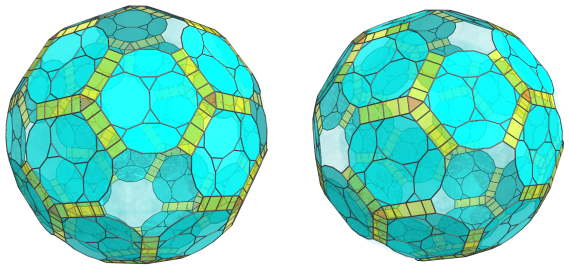
These triangular prisms appear foreshortened into triangles; in 4D they are perfectly uniform triangular prisms.

These aren't the only triangular prisms on the equator; there are 60 other triangular prisms, in a different orientation, that share an edge with one of the 30 truncated dodecahedra:

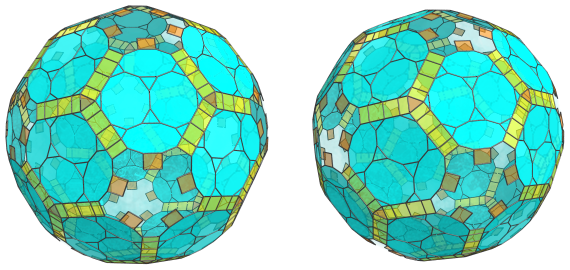
These triangular prisms, due to being in a different orientation, have been foreshortened into rectangles. They are nevertheless uniform triangular prisms just like the previous ones. They also alternate with cuboctahedra, 60 of which lie on the equator:

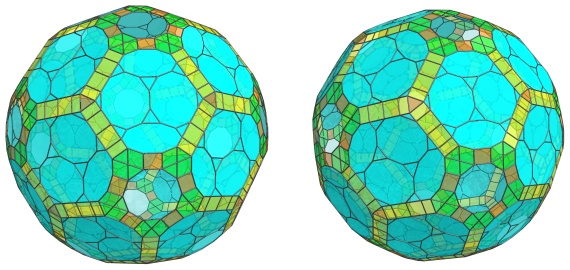
These cuboctahedra have also been foreshortened, into hexagons. They are, of course, perfectly uniform in 4D.

Finally, the remaining decagonal gaps are filled in by 12 more decagonal prisms:

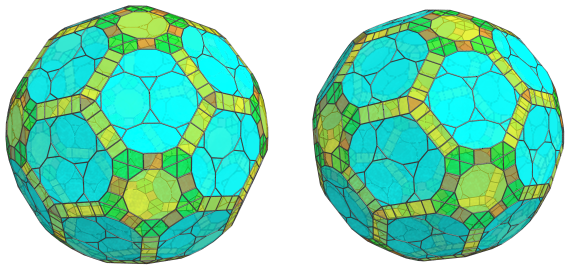
These decagonal prisms are in a different orientation from the other decagonal prisms we saw on the equator, so they have been foreshortened into decagons rather than rectangles.

These are all the cells that lie on the equator of the runcitruncated 120-cell. Past this point, the arrangement of cells mirrors that of the cells on the near side that we have seen earlier, repeating in reverse until it reaches the antipodal truncated dodecahedron.

Summary

The following table summarizes the cell counts of each layer of the runcitruncated 120-cell:

Region	Layer
Near side	1	1	12	30	20
	2	12	30	20	20
	3	20	60 + 12 = 72	60 + 60 + 60 = 180	30 + 60 = 90
	4	12	30 + 60 = 90	60 + 30 = 90	60
	5	0	120	120 + 120 = 240	60 + 20 = 80
	Subtotal	45	324	560	270
Equator		30	60 + 12 = 72	20 + 60 = 80	60
Far side	5	0	120	240	80
	4	12	90	90	60
	3	20	72	180	90
	2	12	30	20	20
	1	1	12	30	20
	Subtotal	45	324	560	270
Grand total		120	720	1200	600

Coordinates

The coordinates of an origin-centered runcitruncated 120-cell with edge length 2 are all permutations of coordinates and changes of sign of:

• (0, 2, 2φ⁴, 2φ⁴)
• (1, 1, 3φ³, 5+6φ)
• (1, 1, 1+4φ, φ⁶)
• (φ³, 3+2φ, 3φ³, 3φ³)
• (2φ², 2φ², 2+6φ, 2φ⁴)

as well as even permutations of coordinates and all changes of sign of:

(0, 1, 4+9φ, 1+3φ) (0, 2+φ, 3+7φ, 3φ3) (0, φ3, 6+7φ, 3φ2) (0, 3φ, 5+7φ, 3+4φ) (1, 4φ2, φ5, 4+5φ) (1, φ2, 4+7φ, 2+6φ) (1, φ2, 6+7φ, 2φ3) (1, φ2, 4+9φ, 2φ2) (1, 2φ, 5+7φ, 2+5φ) (1, φ3, φ6, 3+2φ) (1, 2φ2, 3+7φ, 4+5φ) (1, 1+3φ, 4+7φ, 4φ2) (2, φ2, φ6, φ4) (2, φ3, 4+7φ, φ5) (φ2, 2+5φ, 3φ3, 4φ2) (φ2, 2φ, 4+9φ, φ3) (φ2, 3φ, φ6, 2φ2) (φ2, 3+2φ, 2φ4, 4+5φ)

(φ2, φ4, 5+6φ, 4φ2) (φ2, 3+4φ, 2+6φ, 4+5φ) (2φ, 2+φ, 1+3φ, φ6) (2φ, 3φ2, 3φ3, 4+5φ) (2φ, 2φ3, 2φ4, 4φ2) (2+φ, 2φ2, 5+6φ, φ5) (φ3, 2+5φ, 2+6φ, φ5) (φ3, 2φ2, 1+3φ, 6+7φ) (φ3, 1+4φ, 5+6φ, 3+4φ) (3φ, 2φ3, 3φ3, φ5) (2φ2, 1+3φ, 5+6φ, 2+5φ) (2φ2, 3+2φ, φ4, 5+7φ) (2φ2, 1+4φ, 4+7φ, 3φ2) (1+3φ, 3+2φ, 2φ3, 4+7φ) (1+3φ, φ4, 3φ3, 2+6φ) (1+3φ, 1+4φ, 2φ4, 2+5φ) (φ4, 1+4φ, 3+7φ, 2φ3)

where φ=(1+√5)/2 is the Golden Ratio.