The Truncated Dodecahedron

---

The truncated dodecahedron is a 3D uniform polyhedron bounded by 32 polygons (20 triangles and 12 decagons), 90 edges, and 60 vertices. It may be constructed by truncating the dodecahedron's vertices such that its pentagonal faces become decagons. Alternatively, it may be constructed by radially expanding the edges of the dodecahedron outwards, thus turning vertices into triangles and pentagons into decagons.

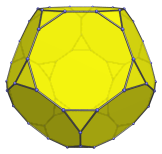
The truncated dodecahedron may be augmented by a pentagonal cupola (J5) to form an augmented truncated dodecahedron (J68), one of the Johnson solids. A second augment can be added to the opposite decagon to produce the parabiaugmented truncated dodecahedron (J69), or to a non-opposite, non-adjacent decagon to produce the metabiaugmented truncated dodecahedron (J70). The latter can be further augmented with a third pentagonal cupola to produce the triaugmented truncated dodecahedron (J71).

Projections

In order to be able to identify the truncated dodecahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:

Projection	Envelope	Description
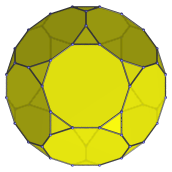	Dodecagon	Parallel projection centered on a decagonal face.
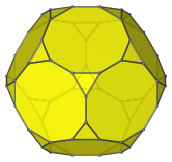	Icositetragon	Parallel projection centered on a triangular face.
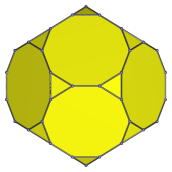	Non-uniform decagon	Parallel projection centered on an edge shared between two decagons.
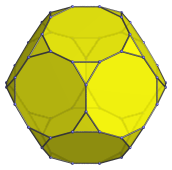	Icositetragon	Vertex-centered parallel projection.

Coordinates

The Cartesian coordinates of the truncated dodecahedron, centered on the origin and having edge length 2, are all even permutations of coordinates and changes of sign of:

• (0, 1+3φ, 1)
• (1, 2φ², φ²)
• (φ², φ³, 2φ)

where φ=(1+√5)/2 is the Golden Ratio.

Occurrences

The truncated dodecahedron occurs as cells in the following uniform polychora:

• The truncated 120-cell;
• The runcitruncated 120-cell.