The Rhombicosidodecahedron

---

The rhombicosidodecahedron, also known as the small rhombicosidodecahedron, is a 3D uniform polyhedron bounded by 62 polygons (20 triangles, 30 squares, and 12 pentagons), 120 edges, and 60 vertices. It may be constructed by radially expanding the pentagonal faces of the dodecahedron outwards, or equivalently, the triangular faces of the icosahedron outwards.

The 12 pentagonal faces correspond with the faces of the dodecahedron, the 20 triangular faces correspond with the faces of the icosahedron, and the 30 square faces correspond with the edges of both the dodecahedron and the icosahedron.

Projections

In order to be able to identify the rhombicosidodecahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:

Projection	Envelope	Description
	Decagon	Parallel projection centered on a pentagonal face. The edges of the projection are the images of 10 of the square faces.
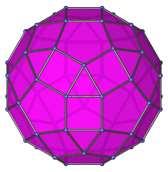	Dodecagon	Parallel projection centered on a triangular face.
	Dodecagon	Parallel projection centered on a square face.
	Tetradecagon	Vertex-centered parallel projection.

Coordinates

The Cartesian coordinates of the rhombicosidodecahedron, centered on the origin and having edge length 2, are all permutations of coordinates and changes of sign of:

• (1, 1, φ³)

together with all even permutations of coordinates and changes of sign of:

• (0, φ², φ√5)
• (φ, 2φ, φ²)

where φ=(1+√5)/2 is the Golden Ratio.

Occurrences

The rhombicosidodecahedron occurs as cells in the following uniform polychora:

• The cantellated 120-cell;
• The runcitruncated 600-cell.

It also occurs in the following CRF polychora:

• The castellated rhombicosidodecahedral prism.