The Truncated Octahedron

---

The truncated octahedron is a 3D uniform polyhedron bounded by 14 polygons (8 hexagons and 6 squares), 36 edges, and 24 vertices. It may be constructed by truncating the octahedron at 1/3 of its edge length.

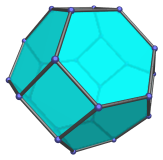
The dual of the truncated octahedron is the tetrakis hexahedron, a Catalan solid.

Projections

In order to be able to identify the truncated octahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:

Projection	Envelope	Description
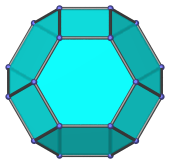
	Octagon	Parallel projection centered on a square face. The top, bottom, left, and right edges of the projection envelope are images of square faces.
	Dodecagon	Parallel projection centered on a hexagonal face.
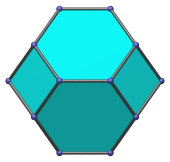	Hexagon	Parallel projection centered on an edge between two hexagons. The top and bottom edges of the projection envelope are images of square faces.
	Non-uniform decagon	Parallel projection centered on a vertex.

Coordinates

The Cartesian coordinates of the truncated octahedron, centered on the origin and having edge length 2, are all permutations of coordinates and changes of sign of:

• (0, √2, 2√2)

Occurrences

The truncated octahedron appears as cells in the following 4D uniform polytopes:

• The cantitruncated 5-cell;
• The omnitruncated 5-cell;
• The bitruncated tesseract;
• The omnitruncated tesseract;
• The truncated 24-cell;
• The runcitruncated 24-cell;
• The cantitruncated 600-cell;
• The omnitruncated 120-cell.

It also occurs as cells in the following CRF polychora:

• The tetrahedral canticupola (K4.76);
• The augmented cantitruncated 5-cell.