The Truncated Tetrahedron

---

The truncated tetrahedron is a 3D uniform polyhedron bounded by 8 polygons (4 hexagons and 4 triangles), 18 edges, and 12 vertices. It is the simplest of the Archimedean polyhedra. It may be constructed by truncating the tetrahedron at 1/3 of its edge length.

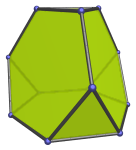
Six of the edges of the truncated tetrahedron correspond with the 6 edges of the tetrahedron.

The truncated tetrahedron can be augmented with a triangular cupola (J3) to produce the augmented truncated tetrahedron (J65), a Johnson solid.

The dual of the truncated tetrahedron is the triakis tetrahedron, a Catalan solid.

Projections

In order to be able to identify the truncated tetrahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:

Projection	Envelope	Description
	Non-uniform nonagon	Parallel projection centered on a triangular face.
	Non-uniform nonagon	Parallel projection centered on a hexagonal face.
	Octagon	Parallel projection centered on an edge shared by two hexagons.
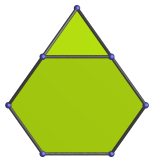	Non-uniform pentagon	Parallel projection parallel to three edges: one between two hexagonal faces and two between a hexagon and a triangle each. The images of many faces coincide: the top and bottom halves of the image are the images of two triangles and two hexagons, respectively. The other faces project to the edges of the projection envelope: two hexagons to the top left and right edges, and two triangles to the bottom left and right edges. The top vertex of the projection envelope is the image of an edge. This projection of the truncated tetrahedron appears in the icosahedron-centered projection of the truncated 600-cell.
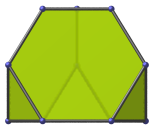	Non-uniform hexagon	Parallel projection parallel to a hexagonal face and a triangular face.

Coordinates

The Cartesian coordinates for the truncated tetrahedron, centered on the origin and having edge length 2 are:

• (1/√6, −2/√3, ±2)
• (1/√6, 4/√3, 0)
• (−3/√6, 0, ±2)
• (−3/√6, ±3/√3, ±1)
• (5/√6, −1/√3, ±1)
• (5/√6, 2/√3, 0)

These coordinates give an “upright” truncated tetrahedron, in the sense that one of its hexagonal faces is orthogonal to the X-axis. They are obtained by radially expanding the edges of a tetrahedron outwards such that the resulting polyhedron has equal edge lengths.

Occurrences

The truncated tetrahedron occurs as cells in many uniform polychora:

• The truncated 5-cell, which is its closest 4D analogue;
• The bitruncated 5-cell, whose surface consists solely of truncated tetrahedra;
• The runcitruncated 5-cell;
• The cantitruncated 5-cell;
• The truncated 16-cell;
• The bitruncated tesseract;
• The runcitruncated 16-cell;
• The cantitruncated tesseract;
• The truncated 600-cell.
• The bitruncated 120-cell;
• The cantitruncated 120-cell;
• The runcitruncated 600-cell.

It also occurs in the following CRF polychora:

• The truncated tetrahedral cupoliprism (K4.55);
• The tetrahedral canticupola (K4.76);
• The tetrahedral magnaursachoron;
• The augmented cantitruncated 5-cell;
• The octa-augmented runcitruncated 16-cell;
• The runcinated snub 24-cell.