The Truncated Tetrahedral Cupoliprism
The truncated tetrahedral cupoliprism, also variously known as the parabidiminished rectified tesseract, truncated tetrahedron atop inverted truncated tetrahedron, the Bowers acronym tutcup, or K4.55 in Klitzing's list of segmentochora, is a CRF polychoron formed from the convex hull of two truncated tetrahedra placed in dual orientation to each other in parallel hyperplanes, with 6 tetrahedra and 8 triangular cupolae connecting them. It has a total of 16 cells, 52 polygons (32 triangles, 12 squares, 8 hexagons), 60 edges, and 24 vertices.
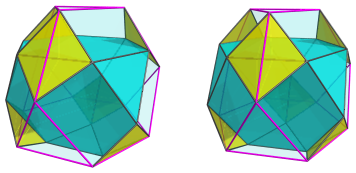
Even though it is not uniform because of the triangular cupola cells, it is nonetheless vertex-transitive, and thus belongs in the category of scaliform polytopes.
Structure
We shall explore the structure of tutcup using its parallel projections into 4D, centered on a truncated tetrahedral cell.

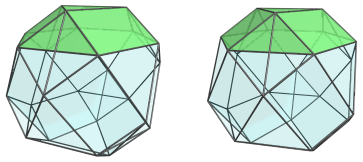
The above image shows the nearest truncated tetrahedron to the 4D viewpoint. For clarity, we have left out the other cells.
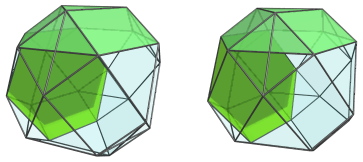
The hexagonal faces of this truncated tetrahedron are joined to 4 triangular cupolae, shown next:
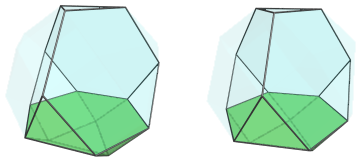


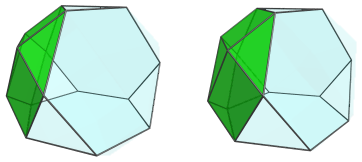
Here are all the cells together:
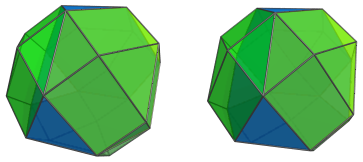
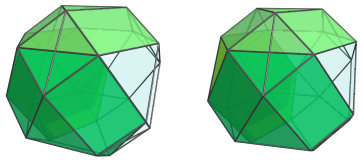
Where the triangular faces of the cupolae touch each other, are 6 tetrahedral cells:

These tetrahedra have been foreshortened into squares because they lie at a 90° angle to the 4D viewpoint. But in reality, they are perfectly regular tetrahedra. For clarity, we've left the cells on the near side of the polychoron only in edge outline.
The far side of these tetrahedra are joined to 4 more triangular cupolae on the far side of the polytope:
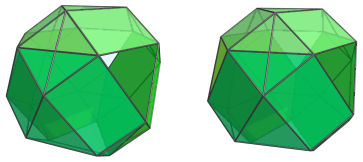
The cavity surrounded by these cupolae are filled by the antipodal truncated tetrahedron:

Here are all the far side cells together:

The following table summarizes the cell counts for the truncated tetrahedral cupoliprism:
| Region | |||
|---|---|---|---|
| Near side | 1 | 0 | 4 |
| Equator | 0 | 6 | 0 |
| Far side | 1 | 0 | 4 |
| Grand total | 2 | 6 | 8 |
| 16 cells | |||
Coordinates
The Cartesian coordinates of tutcup (K4.55), centered on the origin with edge length 2, are:
- (±1, −1/√3, 5/√6, 1/√2)
- (0, 2/√3, 5/√6, 1/√2)
- (±2, −2/√3, 1/√6, 1/√2)
- (0, 4/√3, 1/√6, 1/√2)
- (±1, ±3/√3, −3/√6, 1/√2)
- (±2, 0, −3/√6, 1/√2)
- (±1, ±3/√3, 3/√6, −1/√2)
- (±2, 0, 3/√6, −1/√2)
- (±2, 2/√3, −1/√6, −1/√2)
- (0, −4/√3, −1/√6, −1/√2)
- (±1, 1/√3, −5/√6, −1/√2)
- (0, −2/√3, −5/√6, −1/√2)




