The Deca-augmented 5,20-duoprism
The deca-augmented 5,20-duoprism is a CRF polychoron bounded by 5 icosagonal prisms, 50 square pyramids, and 10 elongated pentagonal bipyramids (J16) for a total of 65 cells, with 255 polygons (150 triangles, 100 squares, and 5 icosagons), 300 edges, and 110 vertices.

It is constructed by augmenting the 5,20-duoprism with 10 pentagonal prism pyramids on alternating pentagonal prisms. Due to the dichoral angle between the pentagonal prisms in the 5,20-duoprism being exactly 162°, and the dichoral angle between the pentagonal pyramids and pentagonal prism of the pentagonal prism pyramid being exactly 18°, the pentagonal pyramid cells of the 10 augments lie on the same hyperplanes as the adjacent pentagonal prism cells, and merge with them to form 10 elongated pentagonal bipyramids (J16).
Structure
Centered on an Icosagonal Prism
The structure of the ring of 5 icosagonal prisms is identical to the underlying 5,20-duoprism:





The toroidal gap left by these icosagonal prisms are filled with a ring of 10 elongated pentagonal bipyramids (J16) cells that touch each other at their apices:

These J16 cells appear somewhat flattened by perspective foreshortening, because they lie at a steep angle to the 4D viewpoint. They are, of course, undistorted J16 cells in 4D.
Surrounding the apices of each pair of adjacent J16 cells are florets of square pyramids:





These square pyramids are also foreshortened into various squished pyramids because they lie at the same steep angles to the 4D viewpoint as the J16 cells.
Centered on an Elongated Pentagonal Bipyramid
The Near Side
We now examine the structure of the deca-augmented 5,20-duoprism from a different viewpoint that better shows the J16 and square pyramid cells.

The above image shows 5 of the J16 cells facing the 4D viewpoint. The top and bottom J16 cells appear squished; this is foreshortening caused by their leaning into the 4th dimension. In 4D they are undistorted Johnson solids.
Between each adjacent pair of J16 cells are 5 square pyramids bridging them, for a total of 20 square pyramids on the near side:

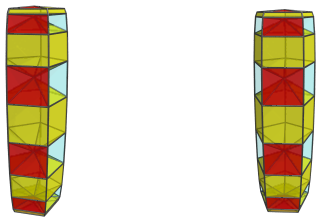



These are all the cells that lie on the near side of the augmented duoprism.
The Far Side
On the far side are the other 5 J16 cells:

Here are the rest of the square pyramids that straddle these J16 cells:





Just like the cells on the near side, these cells appear more and more foreshortened towards the top and bottom of the projection image, because there they gradually bend away into the 4th dimension along the icosagonal surface of the duoprism.
The next images show the icosagonal prisms that form the orthogonal ring of the duoprism, wrapping around this column of cells:





These icosagonal prisms appear squished into narrow strips, because they lie almost at a 90° angle to the 4D viewpoint. They are, of course, perfectly uniform icosagonal prisms, and their steep curvature into the 4th dimension, as implied by this extreme foreshortening, gives an indication of how the column of J16 and square pyramid cells above bend into the 4th dimension.
Summary
The following table summarizes the cell counts for this 4D viewpoint of the deca-augmented 5,20-duoprism:
| Region | |||
|---|---|---|---|
| Near side | 5 | 20 | - |
| Far side | 5 | 30 | 5 |
| Grand total | 10 | 50 | 5 |
| 65 cells | |||
Coordinates
The Cartesian coordinates of the deca-augmented 5,20-duoprism, centered on the origin and with edge length 2, are:
- (0, ±A, F, 0)
- (±A, 0, F, 0)
- (±B, ±C, F, 0)
- (±C, ±B, F, 0)
- (±D, ±E, F, 0)
- (±E, ±D, F, 0)
- (0, ±A, G, ±φ)
- (±A, 0, G, ±φ)
- (±B, ±C, G, ±φ)
- (±C, ±B, G, ±φ)
- (±D, ±E, G, ±φ)
- (±E, ±D, G, ±φ)
- (0, ±A, H, ±1)
- (±A, 0, H, ±1)
- (±B, ±C, H, ±1)
- (±C, ±B, H, ±1)
- (±D, ±E, H, ±1)
- (±E, ±D, H, ±1)
- ±(P, Q, 0, 0)
- ±(R, R, 0, 0)
- ±(Q, P, 0, 0)
- ±(−S, T, 0, 0)
- ±(−T, S, 0, 0)
where:
| A | = | 2√(2φ2+√(11φ+7)) |
| B | = | √(2+√(φ+2)) |
| C | = | √(6+8φ+√(145φ+90)) |
| D | = | √(4+2φ+√(20φ+15)) |
| E | = | √(4+6φ+√(76φ+47)) |
| F | = | √((10+2√5)/5) |
| G | = | √((5−√5)/10) |
| H | = | −√((5+2√5)/5) |
| P | = | √(13+19/√5+√((481+991/√5)/2)) |
| Q | = | √(1−1/√5+√((5−√5)/10)) |
| R | = | √(7+9/√5+8√(1+2/√5)) |
| S | = | √(5−1/√5+√(25−2√5)) |
| T | = | √(9+19/√5+3√(17+38/√5)) |
and φ=(1+√5)/2 is the Golden Ratio.




