The Bilunabirotunda Pseudo­pyramid

---

The bilunabirotunda pseudopyramid, or J91 pseudopyramid for short, is a CRF polychoron belonging to the family of pseudopyramids, polytopes that are derived from true pyramids by a modified form of Stott expansion, consisting of a base facet and lateral facets that taper to a subdimensional apex that is not necessarily a point. It consists of a bilunabirotunda (J91) base, and 4 tetrahedra, 4 square pyramids, 4 pentagonal pyramids, and 2 triangular prisms that taper to a single edge above the J91. It has a total of 15 cells, 42 polygons (32 triangles, 6 squares, 4 pentagons), 43 edges, and 16 vertices.

It was discovered on 23 Feb 2014 by W. Gevaert of Netherlands (aka student91).

Construction

One possible construction is via the so-called EKF process (Expanded Kaleido-Faceting), applied to the icosahedral pyramid. This is the same process that derives the bilunabirotunda from the icosahedron:

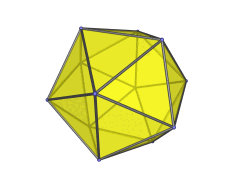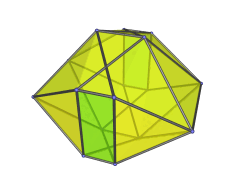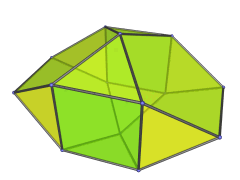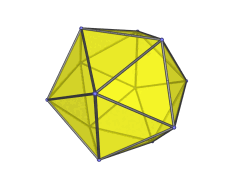
The icosahedron is faceted according to one of its subsymmetries, yielding a non-convex polyhedron, and then Stott expansion is applied to make it convex again. Applied to the icosahedral pyramid, this process turns the icosahedral base into a bilunabirotunda, while the apex of the pyramid is lengthened from a point to a unit edge. Four of the 20 tetrahedra are preserved, while the rest are deformed into or replaced with the other cells found in the J91 pseudopyramid.

Structure

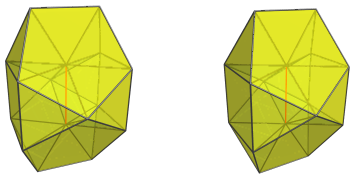
We shall explore the structure of the J91 pseudopyramid via its parallel projections into 3D.

The red vertical edge in the above image is the apex of the pseudopyramid, and is the part closest to the 4D viewpoint.

Surrounding this edge are two triangular prisms:

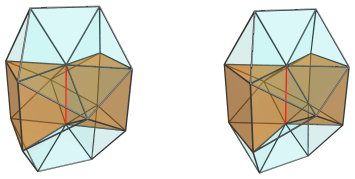
and 4 square pyramids:

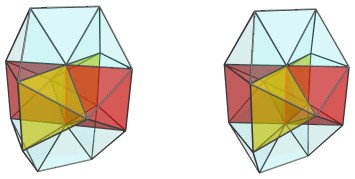
Touching either end of this apical edge are 4 tetrahedra:

as well as 4 pentagonal pyramids, two of which are shown next:

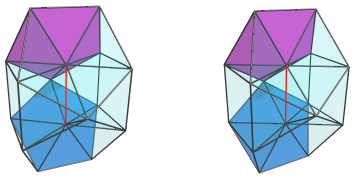
and the other two:

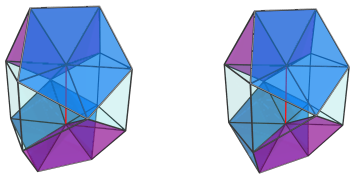
Finally, of course, here is the bilunabirotunda itself, as the base of the pyramid:

Coordinates

The Cartesian coordinates of the J91 pseudopyramid, having edge length 2, are:

• (±1, 0, ±φ², 0)
• (±φ, ±1, ±1, 0)
• (0, ±φ, 0, 0)
• (0, 0, ±1, 1/φ)

where φ=(1+√5)/2 is the Golden Ratio.

Like the icosahedral pyramid from which it derives, the J91 pseudopyramid is quite shallow, having a height of only 1/φ (approx. 0.61803) for an edge length of 2.