The Tetrahedron

---

The regular tetrahedron is the 3D equivalent of the triangle. It is the simplest of the Platonic solids, and consists of 4 equilateral triangles joined at their edges, folded into 3D to form a pyramid with a triangular base.

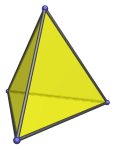
It has 4 vertices and 6 edges. It is self-dual: the polyhedron formed by taking the convex hull of the center points of each face is also a tetrahedron.

The tetrahedron occurs as cells in the pentachoron, the 16-cell, and the 600-cell. It also occurs as cells in many of the uniform polytopes. The full list is given below.

Two tetrahedra can be attached, face-to-face, to form the triangular bipyramid (J12), a Johnson solid.

A tetrahedron can be used to augment a tridiminished icosahedron (J63) to form the augmented tridiminished icosahedron (J64).

Projections

In order to be able to identify the tetrahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:

Projection	Envelope	Description
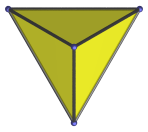	Equilateral triangle	Vertex-first parallel projection.
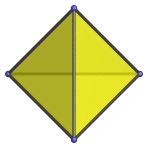	Square	Edge-first parallel projection.
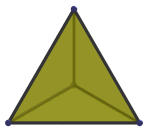	Equilateral triangle	Face-first parallel projection.
	Isosceles triangle	Parallel projection with view angle parallel to an edge. This edge appears as the top point of the triangular projection image. The two slanting sides of the projection envelope are the images of two of the faces.
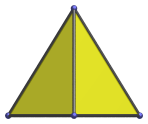	Iscosceles triangle	Parallel projection with view angle parallel to base, passing through the center and intersecting an edge. The bottom edge of the image is the image of the bottom face of the tetrahedron.

Coordinates

There are two ways of obtaining coordinates for the tetrahedron.

As the Alternation of the Cube

The first way is to make use of the fact that it is the alternation of the cube: take a cube and color its vertices red or green, such that every edge connects a red vertex to a green vertex. This partitions the cube's 8 vertices into two groups of 4 each. The convex hull of each set of 4 vertices is a tetrahedron. The two tetrahedra obtained by taking the convex hull of one or the other set of 4 vertices are dual to each other.

This process of coloring the cube's vertices is equivalent to partitioning the cube's vertices according to whether they have an odd number of negative signs or an even number, if we take the cube's coordinates to be (±1, ±1, ±1). This gives us the coordinates of the two tetrahedra as:

1. First tetrahedron:

   • (1, 1, 1)
   • (−1, −1, 1)
   • (−1, 1, −1)
   • (1, −1, −1)

2. Second tetrahedron:

   • (−1, 1, 1)
   • (1, −1, 1)
   • (1, 1, −1)
   • (−1, −1, −1).

These coordinates give tetrahedra with edge length 2√2.

As a Triangular Pyramid

The coordinates of the tetrahedron may also be obtained by starting with an equilateral triangle and adding an apex equidistant from the triangle's vertices. Given an origin-centered equilateral triangle having edge length 2 with the coordinates (±1, −1/√3), (0, 2/√3), we add a fourth vertex equidistant from these coordinates, of the form (0, 0, k). A little trigonometry shows that in order for the resulting tetrahedron to be regular, the height of this fourth vertex must be 4/√6 units above the equilateral triangle. This gives the coordinates of the tetrahedron as (±1, −1/√3, 0), (0, 2/√3, 0), (0, 0, 4/√6). A little more trigonometry shows that in order to center this tetrahedron on the origin, we need to translate it by (0, 0, -1/√6), thus yielding the coordinates:

• (±1, −1/√3, −1/√6)
• (0, 2/√3, −1/√6)
• (0, 0, 3/√6)

The resulting tetrahedron has edge length 2.

These coordinates in themselves may appear less regular than the ones derived by alternating the cube. However, they are part of a general pattern that extends to all dimensions, whereas the derivation by alternating the cube has no analogue in all other dimensions. They also have the property that the base of the resulting tetrahedron is parallel to the XY plane, which is convenient for orienting the tetrahedron in 3D modelling scenes.

Occurrences

The tetrahedron occurs as cells in the following regular polychora:

• The 5-cell, its direct 4D analogue;
• The 16-cell;
• The 600-cell.

It also occurs in the following uniform polychora:

• The truncated 5-cell;
• The rectified 5-cell;
• The runcinated 5-cell;
• The truncated tesseract;
• The rectified tesseract;
• The runcincated tesseract;
• The snub 24-cell;
• The rectified 120-cell;
• The truncated 120-cell;
• The runcinated 120-cell;
• The grand antiprism.

as well as many CRF polychora, generalizations of the Johnson solids to 4D, including (but not limited to) the following:

• Cube antiprism (K4.15);
• Cube atop icosahedron (K4.21);
• Cube atop cuboctahedron;
• The truncated tetrahedral cupoliprism;
• The octa-augmented runcinated tesseract;
• The octa-augmented truncated tesseract;
• The castellated rhombicosidodecahedral prism;
• The triangular hebesphenorotundaeic rhombochoron;
• The tetrahedral ursachoron;
• The bilunabirotunda pseudopyramid;
• The pentagonorhombic trisnub trisoctachoron (D4.11).