The Pentagonorhombic Trisnub Trisoctachoron

---

The Pentagonorhombic Trisnub Trisoctachoron (D4.11), also known by its Bowers' Acronym pretasto, is a CRF polychoron with demitesseractic symmetry that has a surface containing 144 cells (24 bilunabirotundae (J91), 8 cuboctahedra, 40 octahedra, 32 tridiminished icosahedra (J63), and 40 tetrahedra), 592 polygons (96 pentagons, 48 squares, and 448 triangles), 624 edges, and 176 vertices. It was discovered on 12 Mar 2014.

Its primary point of interest lies in its 24 bilunabirotunda (J91) cells, which are transitive under its demitesseractic symmetry and therefore correspond with the icosahedra of the snub 24-cell. It can be constructed from the snub 24-cell using a kaleido-faceting operation followed by a partial Stott expansion that restores convexity.

These J91 cells can be augmented with J91 pseudopyramids, whose pentagonal pyramid cells will lie in the same hyperplanes as the J63 cells, thus augmenting them into icosahedra. The resulting polychoron is CRF, has demitesseractic symmetry, and sports 32 icosahedral cells.

Structure

We shall explore the structure of D4.11 using its parallel projections into 3D.

The Near Side

The above image shows the tetrahedral cell nearest to the 4D viewpoint. For the sake of clarity, we render all other cells in a light transparent color.

The edges of this tetrahedron are joined to 6 bilunabirotundae (J91):

Note the alternating orientation of these pairs of J91 cells, which indicates the underlying demitesseractic symmetry of the polytope as a whole.

The vertices of the nearest tetrahedron are joined to 4 other tetrahedra:

For clarity, we omit the J91 cells here.

These tetrahedra each belong to a cluster of cells that contain 4 tetrahedra surrounding a cuboctahedron. The corresponding cuboctahedra are shown next:

Three of the other triangular faces of these cuboctahedra are joined to other tetrahedra, for a total of 12 more tetrahedra:

These latest tetrahedra lie at a sharper angle to the 4D viewpoint, and therefore appear flattened by foreshortening. They are, of course, perfectly regular in 4D.

These clusters that each consist of cuboctahedron and 4 tetrahedra are symmetric to each other with respect to the underlying demitesseractic symmetry. There are 8 such groups in the polychoron; these 4 lie on the near side, facing the current 4D viewpoint, and the other 4 lie on the far side.

The tetrahedra directly touching these cuboctahedra are distinguished from the nearest tetrahedron in the center of the projection. We may call them tetrahedra of the second kind, whereas the tetrahedron in the center of the projection, which is part of a set of 8 equivalent tetrahedra, can be termed tetrahedra of the first kind. As we shall see, tetrahedra of the first kind only share edges with the J91 cells; whereas tetrahedra of the second kind share faces with the J91 cells.

Coming back to the nearest tetrahedron, its 4 faces are joined to 4 tridiminished icosahedra (J63):

Again, for clarity, we omit the other cells seen so far, except for the central tetrahedron itself, for reference.

The pentagonal faces of these J63 cells are joined to the bilunabirotundae we saw earlier. Here they are for reference:

The exposed triangular faces of the J63 cells are joined to clusters of octahedra, each having 5 octahedra: one central octahedron surrounded by 4 others in tetrahedral formation. The next image shows the central octahedra:

The lateral octahedra surrounding these central octahedra are shown next:

The remaining exposed faces of the central octahedra are joined to more J63 cells. Together with the J63 cells we saw earlier, these J63 cells surround each central octahedron in tetrahedral formation, in dual orientation to the lateral octahedra.

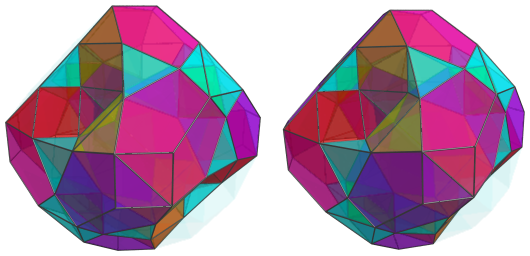
Next, we add the cells from the clusters of cuboctahedra and tetrahedra that we saw earlier:

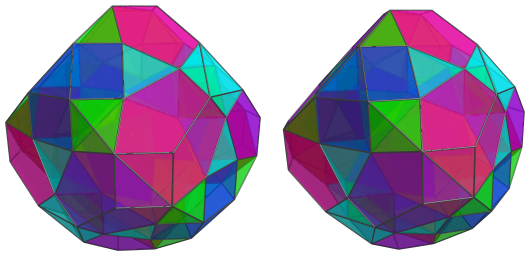
These are all the cells that lie on the near side of the polytope.

The Equator

Now we come to the equator of the polychoron. There are 6 tetrahedra that lie on the equator:

These tetrahedra lie at a 90° angle to the 4D viewpoint, and therefore appear foreshortened into squares. They are, of course, regular tetrahedra in 4D. They are all tetrahedra of the first kind, as defined earlier.

There are also 12 bilunabirotundae (J91) on the equator:

These J91 cells have been foreshortened to octagons because they lie at a 90° angle to the 4D viewpoint.

The 8 remaining triangular gaps above are not the images of any cell; they are where the cuboctahedra on one side of the polytope touch the lateral octahedra on the other side.

The Far Side

Now we come to the far side of the polytope. It has the same arrangement as the near side of the polytope, except in complementary orientation, due to its demitesseractic symmetry.

Here is the farthest tetrahedron, antipodal to the first tetrahedron we saw earlier. Notice how its orientation is dual to the orientation of the first tetrahedron.

Here are the J91 cells on the far side of the polychoron, sharing edges with the farthest tetrahedron:

They are all in the analogous positions as the J91 cells on the near side, except with a different orientation.

The faces of the farthest tetrahedron are shared with 4 J63 cells:

The triangular faces of these J63 cells opposite the tetrahedron are joined to 4 central octahedra, parts of the clusters of 5 octahedra that correspond with the analogous clusters on the near side of the polytope.

Here are the lateral octahedra surrounding these central octahedra, 16 of them in total:

Straddling the edges of the J63 cells, and touching the vertices of the farthest tetrahedron, are 4 more tetrahedra of the second kind:

Their triangular faces opposite the vertices of the farthest tetrahedron are joined to 4 cuboctahedra:

These cells are all filling the gaps between the J91 cells, of course. The next image shows them together:

The remaining exposed triangular faces of these J91 cells are joined to 12 more tetrahedra of the second kind:

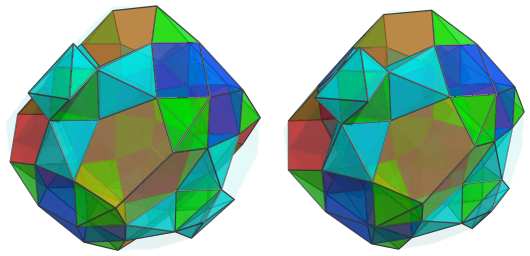
Finally, between the lateral octahedra and the exposed pentagonal faces of the J91 cells are 12 more J63 cells:

These are all the cells that lie on the far side of the polychoron.

Summary

The following table summarizes the cell counts in various regions of D4.11:

Region	Layer
Near side	1	6	-	-	-	1
	2	-	-	-	-	4
	3	-	4	-	-	12
	4	-	-	4	4	-
	5	-	-	16	12	-
	Subtotal	6	4	20	16	17
Equator		12	-	-	-	6
Far side	1	6	-	-	-	1
	2	-	-	4	4	-
	3	-	-	16	-	-
	4	-	4	-	-	4
	5	-	-	-	12	12
	Subtotal	6	4	20	16	17
Grand total		24	8	40	32	40
		144 cells

Coordinates

The coordinates of the pentagonorhombic trisnub trisoctachoron, centered on the origin with edge length 2, are all permutations of coordinates and even changes of sign of:

• (1/(φ√2), φ²/√2, φ²/√2, (3+φ)/√2)
• (1/√2, 1/√2, 1/√2, (3+2φ)/√2)
• (φ/√2, φ/√2, (2+φ)/√2, −(2+φ)/√2)

where φ=(1+√5)/2 is the Golden Ratio.