Cube atop Cuboctahedron
Cube atop Cuboctahedron (cube || cuboctahedron), or K4.35, is one of Richard Klitzing's convex segmentochora, 4D CRF polytopes whose vertices lie on two parallel hyperplanes and which are orbiform (can be inscribed into a 4D sphere). It is constructed by placing a cube and a cuboctahedron in two appropriately-spaced parallel hyperplanes and taking their convex hull. Its surface consists of 16 cells (1 cube, 1 cuboctahedron, 6 square antiprisms, 8 tetrahedra), 56 polygons (44 triangles, 12 squares), 60 edges, and 20 vertices.
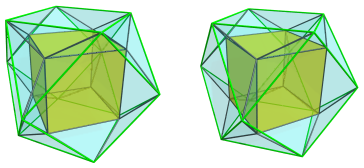
This polychoron is notable for having square antiprisms as cells.
Structure
We shall explore the structure of K4.35 using its parallel projections into 3D.

The above image shows the cubical cell lying on the top hyperplane of the polychoron. Its square faces are joined to 6 square antiprisms:

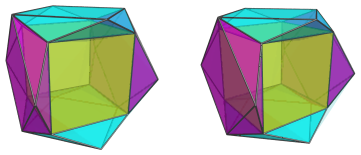
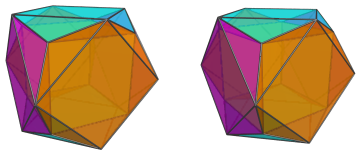
These square antiprisms appear quite flattened, because they lie at an angle to the 4D viewpoint. In 4D, they are perfectly uniform square antiprisms. Their exposed square faces are joined to the antipodal cuboctahedron:

For clarity's sake, we have omitted the cells previously seen.
The triangular faces of this cuboctahedron are joined to 8 tetrahedra:
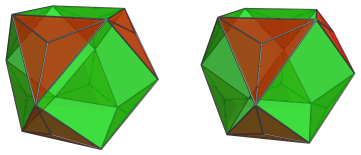
These tetrahedra are foreshortened because they lie at an angle to the 4D viewpoint; in 4D they are perfectly regular tetrahedra.
These are all the cells of K4.35. The following table summarizes the cell counts:
| Region | ||||
|---|---|---|---|---|
| Near side | 1 | 6 | 0 | 0 |
| Far side | 0 | 0 | 8 | 1 |
| Grand total | 1 | 6 | 8 | 1 |
| 16 cells | ||||
Coordinates
The Cartesian coordinates of K4.35, with edge length 2, are:
- (±1, ±1, ±1, √(4√2 - 3))
- (0, ±√2, ±√2, 0)
- (±√2, 0, ±√2, 0)
- (±√2, ±√2, 0, 0)




