The Tetrahedral Magnaursachoron

---

The tetrahedral magnaursachoron is a CRF polychoron consisting of 4 tridiminished rhombicosidodecahedra (J83) in tetrahedral formation around a cuboctahedron, analogous to how J83 itself consists of 3 decagons in triangular formation around a top triangular face.

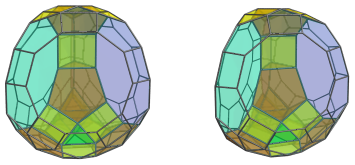
It may be considered as a kind of 4D analogue of J83 itself, having 8 tridiminished icosahedra (J63) and 6 metabidiminished icosahedra (J62) alternating with 34 triangular prisms to fill the gaps in between the J83 cells, and 4 triangular cupolae (J3), 5 cuboctahedra, and a truncated tetrahedron to close up the polytope. It has a total of 62 cells, 272 polygons (124 triangles, 102 squares, 4 hexagons, 36 pentagons, 6 decagons), 342 edges, and 132 vertices.

Structure

We shall explore the structure of the tetrahedral magnaursachoron by means of its parallel projections into 3D.

Top View

We begin with the top view, which best illustrates the tetrahedral symmetry of this polychoron.

The Near Side

The above image shows the nearest cell to the 4D viewpoint: a cuboctahedron, which serves as the top cell of the polychoron. For the sake of clarity, we've culled cells on the far side of the polytope and rendered all the other cells in a light transparent color.

Four of the triangular faces of this cubotahedron are joined to tridiminished icosahedra (J63), shown in the next image:

Between each pair of these J63's, touching the square faces of the cuboctahedron, are 6 triangular prisms:

On the tips of the J63's are 4 more triangular prisms:

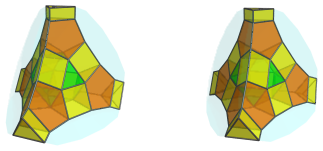
Touching the remaining 4 triangular faces of the cuboctahedron, and covering most of the other cells we've seen so far, are 4 tridiminished rhombicosidodecahedra (J83). For clarity, we show them individually first, and then all together:

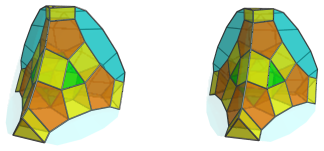
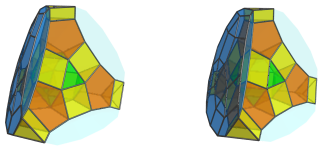
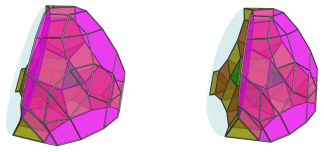
All together:

These J83 cells look very squished due to foreshortening, because they lie at quite a steep angle to the 4D viewpoint. In 4D, of course, they are perfectly undistorted Johnson solids.

These are all the cells that lie on the near side of the polytope from the current 4D viewpoint. Next, we come to the far side.

The Far Side

On the far side of the polychoron is a truncated tetrahedron, which lies antipodal to the cuboctahedron we first saw.

For clarity, we omit the cells on the near side and render the rest of the far side cells in a light transparent color. The triangular faces of this truncated tetrahedron are joined to 4 cuboctahedra:

The hexagonal faces of the truncated tetrahedron are joined to 4 triangular cupolae:

Straddling the cuboctahedra and triangular cupolae are 12 triangular prisms, touching 12 of the edges of the truncated tetrahedron:

The 6 depressions along the remaining exposed edges of the truncated tetrahedron are where 6 metabidiminished icosahedra (J62) are fitted:

The exposed triangular faces of these J62 cells are where another 12 triangular prisms lie:

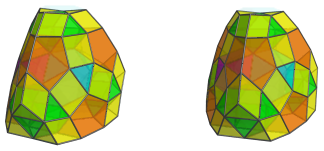
At the tips of this tetrahedral arrangement of cells, where these last triangular prisms cluster in triplets, are the last 4 cells, 4 tridiminished icosahedra (J62):

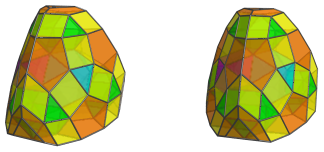
These tridiminished icosahedra look quite squished, because they lie at a steep angle to the 4D viewpoint. In 4D they are, of course, perfectly undistorted Johnson solids.

These are all the cells that lie on the far side of the tetrahedral magnaursachoron.

Summary

The following table summarizes the cell counts of the polytope:

Region	Layer
Near side	1	-	4	-	6	-	1	-
	2	4	-	-	4	-	-	-
Far side	1	-	-	6	12	4	4	1
	2	-	4	-	12	-	-	-
Grand total		4	8	6	34	4	5	1
		62 cells

Side View

The above projections show very clearly the tetrahedral symmetry of the polychoron. However, they don't show as clearly how the curvature of its overall shape resembles the shape of the tridiminished rhombicosidodecahedron (J83) itself. So now we will look at the parallel projections of the tetrahedral magnaursachoron from a side view that better shows this resemblance.

The Near Side

The following image shows one of the cells near the center of the projection, one of the tridiminished icosahedra:

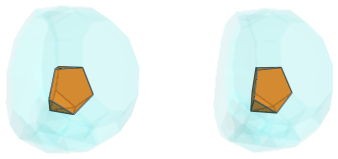
The bottom triangular face of this tridiminished icosahedron is joined to a cuboctahedron:

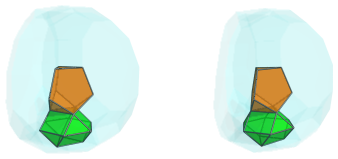
The edges of the bottom triangle in this cuboctahedron touch 3 triangular cupolae:

For clarity's sake, we render the cuboctahedron only in outline. These triangular cupolae appear very squished due to foreshortening, because they lie at almost (but not quite) at a 90° angle to the 4D viewpoint.

The following image shows all the cells so far:

Between the cuboctahedron and these triangular cupolae are 3 triangular prisms:

The other square faces of the cuboctahedron are joined to 3 more triangular prisms, that touch the lateral triangles of the tridiminished icosahedron. There is also a triangular prism that sits atop the tridiminished icosahedron:

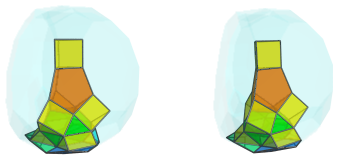
Above the top triangular prism is another tridiminished icosahedron.

Back around the cuboctahedron, the pentagonal depressions formed by the cuboctahedron, triangular cupolae, and triangular prisms are where 3 metabidiminished icosahedra are fitted:

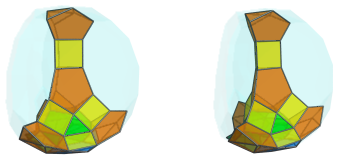
These metabidiminished icosahedra look quite flattened, because they lie at an angle to the 4D viewpoint.

Three triangular prisms are joined to the other side of these metabidiminished icosahedra. Three of the top triangular faces of the top tridiminished icosahedron are also joined to 3 more triangular prisms. These 6 triangular prisms are shown next:

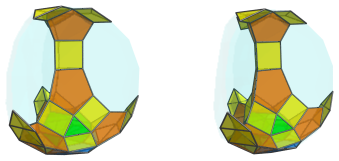
These triangular prisms all lie at rather sharp angles to the 4D line-of-sight, and therefore appear very squished. In 4D, of course, they are perfectly uniform triangular prisms.

These cells are all the framework within which the tridiminished rhombicosidodecahedral (J83) cells are fitted. We show those next:

These J83 cells are folded around the central pillar of alternating triangular prisms and diminished icosahedra, with the cuboctahedron and triangular cupolae at the bottom filling out the gaps between them to close up the polytope.

These are all the cells that lie on the near side of the polychoron.

The Equator

Now we come to the equator of the polytope. These are the cells that lie exactly at a 90° angle from the 4D viewpoint. Two of these cells are the truncated tetrahedron and its antipodal cuboctahedron, shown in the following image:

These cells appear flattened into polygons, because they lie at a 90° angle to the 4D viewpoint.

Around the truncated tetrahedron at the bottom are 6 triangular prisms that also lie on the limb of the polytope, in hexagonal formation:

These triangular prisms have been foreshorted into various irregular pentagons because they lie at a 90° angle to the 4D viewpoint.

These are all the cells that lie on the equator of the tetrahedral magnaursachoron. Past this point, we reach the far side.

The Far Side

On the far side of the polychoron, the primary cell of interest is the last of the 4 tridiminished rhombicosidodecahedra (J83):

This J83 cell occupies most of the projection envelope. Its decagonal faces are joined to the decagonal faces of the other 3 J83 cells on the near side that we saw earlier. The other faces are joined to other cells that fill in the gaps between the J83 cells.

The bottom triangular face is joined to a triangular cupola:

The 15 square faces are joined to 15 triangular prisms:

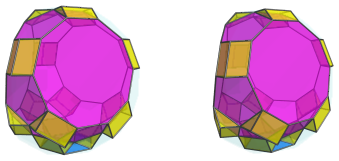
Six of the J83's pentagonal faces are joined to 6 tridiminished icosahedra:

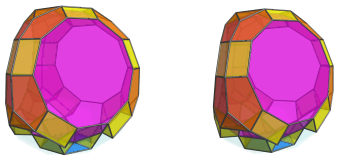
The 3 lower triangular faces are joined to 3 cuboctahedra:

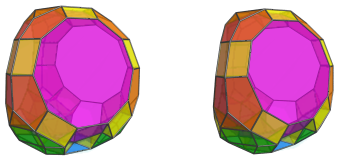
The bottom 3 pentagonal faces are joined to 3 metabidiminished icosahedra:

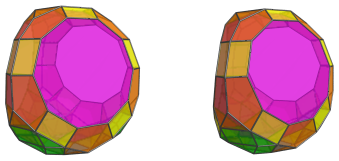
These are all the cells that lie on the far side of the polytope.

Summary

The following table summarizes the cell counts of the polychoron from this side-view:

Region
Near side	3	2	3	13	3	1	-
Equator	-	-	-	6	-	1	1
Far side	1	6	3	15	1	3	-
Grand total	4	8	6	34	4	5	1
	62 cells

Coordinates

The Cartesian coordinates of the tetrahedral magnaursachoron with edge length 2√2 are all even changes of sign of:

• (φ², φ², 1+3φ, 0)
• (φ², 1+3φ, φ², 0)
• (1+3φ, φ², φ², 0)

along with the points:

• (0, ±2, ±2, −3φ²)
• (±2, 0, ±2, −3φ²)
• (±2, ±2, 0, −3φ²)

• (−φ, φ², 3+φ, 2φ)
• (−φ, −φ², −3+φ, 2φ)
• (−1/φ, φ², −3+φ, 2φ)
• (−1/φ, −φ², 3+φ, 2φ)
• (−φ, 3+φ, φ², 2φ)
• (−φ, −3+φ, −φ², 2φ)
• (−1/φ, 3+φ, −φ², 2φ)
• (−1/φ, −3+φ, φ², 2φ)
• (φ², −φ, 3+φ, 2φ)
• (φ², −1/φ, −3+φ, 2φ)
• (−φ², −φ, −3+φ, 2φ)
• (−φ², −1/φ, 3+φ, 2φ)
• (φ², 3+φ, −φ, 2φ)
• (φ², −3+φ, −1/φ, 2φ)
• (−φ², 3+φ, −1/φ, 2φ)
• (−φ², −3+φ, −φ, 2φ)
• (3+φ, −φ, φ², 2φ)
• (3+φ, −1/φ, −φ², 2φ)
• (−3+φ, −φ, −φ², 2φ)
• (−3+φ, −1/φ, φ², 2φ)
• (3+φ, φ², −φ, 2φ)
• (3+φ, −φ², −1/φ, 2φ)
• (−3+φ, φ², −1/φ, 2φ)
• (−3+φ, −φ², −φ, 2φ)

• (1, 1, 3, 3φ)
• (1, −1, −3, 3φ)
• (−1, 1, −3, 3φ)
• (−1, −1, 3, 3φ)
• (1, 3, 1, 3φ)
• (1, −3, −1, 3φ)
• (−1, 3, −1, 3φ)
• (−1, −3, 1, 3φ)
• (3, 1, 1, 3φ)
• (3, −1, −1, 3φ)
• (−3, 1, −1, 3φ)
• (−3, −1, 1, 3φ)

• (1, 1, φ³, −φ⁴)
• (1, −1, −φ³, −φ⁴)
• (−1, 1, −φ³, −φ⁴)
• (−1, −1, φ³, −φ⁴)
• (1, φ³, 1, −φ⁴)
• (1, −φ³, −1, −φ⁴)
• (−1, φ³, −1, −φ⁴)
• (−1, −φ³, 1, −φ⁴)
• (φ³, 1, 1, −φ⁴)
• (φ³, −1, −1, −φ⁴)
• (−φ³, 1, −1, −φ⁴)
• (−φ³, −1, 1, −φ⁴)

• (1, 1, 3+2φ, φ)
• (1, −1, −(3+2φ), φ)
• (−1, 1, −(3+2φ), φ)
• (−1, −1, 3+2φ, φ)
• (1, 3+2φ, 1, φ)
• (1, −(3+2φ), −1, φ)
• (−1, 3+2φ, −1, φ)
• (−1, −(3+2φ), 1, φ)
• (3+2φ, 1, 1, φ)
• (3+2φ, −1, −1, φ)
• (−(3+2φ), 1, −1, φ)
• (−(3+2φ), −1, 1, φ)

• (φ, φ, −2+φ, φ³)
• (φ, −φ, 2+φ, φ³)
• (−φ, φ, 2+φ, φ³)
• (−φ, −φ, −2+φ, φ³)
• (φ, 2+φ, −φ, φ³)
• (φ, −2+φ, φ, φ³)
• (−φ, 2+φ, φ, φ³)
• (−φ, −2+φ, −φ, φ³)
• (2+φ, φ, −φ, φ³)
• (2+φ, −φ, φ, φ³)
• (−2+φ, φ, φ, φ³)
• (−2+φ, −φ, −φ, φ³)

• (√5, φ³, φ³, φ)
• (√5, −φ³, −φ³, φ)
• (−√5, φ³, −φ³, φ)
• (−√5, −φ³, φ³, φ)
• (φ³, √5, φ³, φ)
• (φ³, −√5, −φ³, φ)
• (−φ³, √5, −φ³, φ)
• (−φ³, −√5, φ³, φ)
• (φ³, φ³, √5, φ)
• (φ³, −φ³, −√5, φ)
• (−φ³, φ³, −√5, φ)
• (−φ³, −φ³, √5, φ)

• (φ², φ², 3+φ, −2φ²)
• (φ², −φ², −3+φ, −2φ²)
• (−φ², φ², −3+φ, −2φ²)
• (−φ², −φ², 3+φ, −2φ²)
• (φ², 3+φ, φ², −2φ²)
• (φ², −3+φ, −φ², −2φ²)
• (−φ², 3+φ, −φ², −2φ²)
• (−φ², −3+φ, φ², −2φ²)
• (3+φ, φ², φ², −2φ²)
• (3+φ, −φ², −φ², −2φ²)
• (−3+φ, φ², −φ², −2φ²)
• (−3+φ, −φ², φ², −2φ²)

• (2φ, 2φ, 2φ², −φ²)
• (2φ, −2φ, −2φ², −φ²)
• (−2φ, 2φ, −2φ², −φ²)
• (−2φ, −2φ, 2φ², −φ²)
• (2φ, 2φ², 2φ, −φ²)
• (2φ, −2φ², −2φ, −φ²)
• (−2φ, 2φ², −2φ, −φ²)
• (−2φ, −2φ², 2φ, −φ²)
• (2φ², 2φ, 2φ, −φ²)
• (2φ², −2φ, −2φ, −φ²)
• (−2φ², 2φ, −2φ, −φ²)
• (−2φ², −2φ, 2φ, −φ²)

where φ=(1+√5)/2 is the Golden Ratio.