The Pentagonal Prism Pyramid
The pentagonal prism pyramid, also known K4.141 in Klitzing's list of segmentochora, is a CRF polychoron formed by erecting a pyramid over a pentagonal prism base in 4D space. Its surface consists of a pentagonal prism, 2 pentagonal pyramids, and 5 square pyramids for a total of 8 cells, 22 polygons, 25 edges, and 11 vertices.
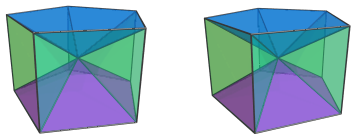
The pentagonal pyramid cells are quite shallow: for edge length 2, their common height is only √((10−2√5)/5), approximately 1.05146, which is barely over half of the edge length; yet their bases are 2 units (1 edge length) apart. For them to meet at a common apex, the height of the pentagonal prism pyramid must therefore be even shallower: √((5−2√5)/5), or approximately 0.324920, only about 16.2% of its edge length.
This shallow height makes it possible for 5,n-duoprisms up to n=20 to be augmented with pentagonal prism pyramids and still remain convex, resulting in a large number of CRF 5,n-duoprism augmentations. The 5,20-duoprism, for example, has 454 distinct augmentations with pentagonal prism pyramids, up to isomorphism.
Furthermore, the angle between the pentagonal pyramid cells and the base pentagonal prism is exactly 18°. When the 5,10-duoprism is augmented by pentagonal prism pyramids, this causes the pentagonal pyramid cells of any adjacent augments to share the same hyperplane, thereby merging into pentagonal bipyramid (J13) cells. Up to 10 augments are possible; the deca-augmented 5,10-duoprism features 10 J13 cells joined apex-to-apex in a ring wrapping around the decagonal prisms.
Similarly, augmenting a 5,20-duoprism with a pentagonal prism pyramid causes the pyramid cells to share the same hyperplane as the adjacent pentagonal prisms of the duoprism, thus merging into elongated pentagonal pyramids (J9). Adding more augments on the other end of the J9 cells turns them into elongated pentagonal bipyramids (J16). Up to 10 augments may be added to the 5,20-duoprism this way: the deca-augmented 5,20-duoprism contains 10 J16 cells joined apex-to-apex into a ring that wraps around the icosagonal prisms.
Structure
We shall explore the pentagonal prism pyramid by means of its parallel projections into 3D. The following image shows a parallel projection of the pentagonal prism pyramid, centered on its apex:

The red vertex in the center of this projection is the apex of the pentagonal prism pyramid. It is the closest vertex to the current 4D viewpoint. Above and below this apex are two pentagonal pyramid cells:
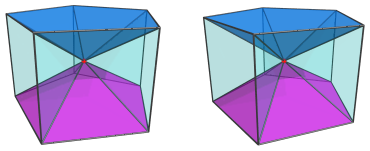
Around the sides, between these pentagonal pyramids, are 5 square pyramids:
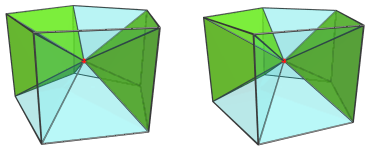
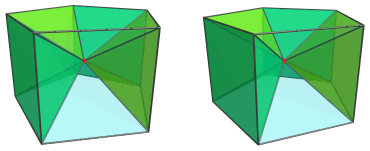
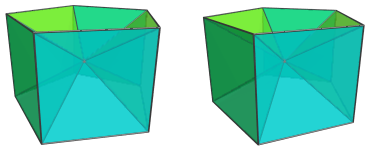
Finally, there is the pentagonal prism cell itself, the base of the pyramid:
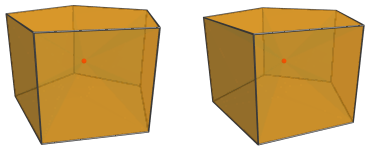
For the sake of clarity, we omit the other cells and edges that don't lie on the pentagonal prism.
Other Projections
The above projections of the pentagonal prism pyramid give a good insight into its structure. However, its pyramid-like shape is not very obvious. So now we turn to its projections from various side-views in 4D.

The above image shows a side-view parallel to the pentagonal faces of the pentagonal prism base, the latter of which projects to a rectangular strip. The blue and magenta triangles are the projections of the two pentagonal pyramids.
It may not be immediately obvious from the 3D vantage point that this projection shows just how shallow the pentagonal prism pyramid is. Here's the same projection seen from a slightly different 3D vantage point (the 4D viewpoint is unchanged):

The very shallow height of the projection, and of the pentagonal prism pyramid itself, should now be obvious.
Here is another side-view projection from a different 4D viewpoint: this time parallel to the axis of the pentagonal prism base. This causes the projection envelope to be a pentagonal pyramid:

The pentagonal base is the projection image of the pentagonal prism.
Unlike the Johnson solid, however, this pentagonal pyramid projection envelope is significantly more shallow, as shown by the next image which moves the 3D viewpoint downwards slightly while retaining the same 4D viewpoint:
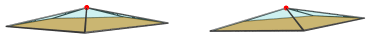
Again, this exemplifies just how shallow the pentagonal prism pyramid is, its height being only about 16.2% of its edge length.
Coordinates
The Cartesian coordinates of the pentagonal prism pyramid (K4.141) with edge length 2 are:
- (0, 0, 0, √((5−2√5)/5))
- (√((10+2√5)/5), 0, ±1, 0)
- (√((5−√5)/10), ±φ, ±1, 0)
- (−√((5+2√5)/5), ±1, ±1, 0)
where φ=(1+√5)/2 is the Golden Ratio.




