The Truncated Tesseract
The truncated tesseract is a relatively simple uniform polychoron bounded by 24 cells (8 truncated cubes, 16 tetrahedra), 88 polygons (64 triangles, 24 octagons), 128 edges, and 64 vertices. It is an analogue of the 3D truncated cube, with its tetrahedra being the analogue of the truncated cube's triangular faces, and its truncated cubes the analogue of the truncated cube's octagonal faces.

Structure
We will explore the structure of the truncated tesseract by using its parallel projection into 3D, centered on a truncated cube:

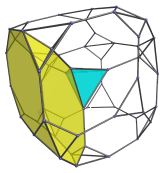
As can be seen, its projection envelope is a cube. Nine cells are visible from this viewpoint: 1 truncated cube (in yellow), and 8 tetrahedra (in cyan). The truncated cube, which we may regard as lying on the “north pole” of the truncated tesseract, is shown on its own below:

The eight gaps are, of course, occupied by 8 tetrahedra:

The six square faces of the projection envelope are, in fact, the images of six truncated cubes, shown below in pairs:

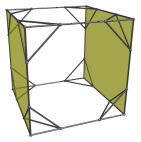
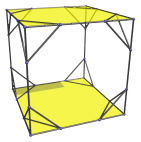
They appear flattened into squares in the projection because they are being viewed from a 90° angle. In reality, they are perfectly uniform truncated cubes. They lie on the “equator” of the truncated tesseract.
On the far side of the truncated tesseract, another 8 tetrahedra are joined to these 6 equatorial cells, as well as the last truncated cube at the “south pole”. These cells have exactly the same arrangement as the “north pole“ truncated cube and the 8 tetrahedra we have seen above.
In total, there are the “north pole” truncated cube, 6 truncated cubes on the equator, and the “south pole” truncated cube, for a total of 8 truncated cubes. There are a total of 8+8=16 tetrahedra.
Perspective Projections
This image shows the perspective projection of the truncated tesseract from another viewpoint, centered on one of the 16 tetrahedra:

For the sake of clarity, we've omitted the cells that lie on the far side of the truncated tesseract. The nearest tetrahedron to the 4D viewpoint lies at the center of the projection envelope, as shown below:

Surrounding it are 4 truncated cubes:
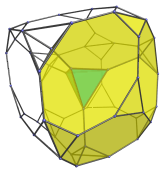
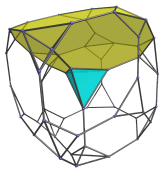
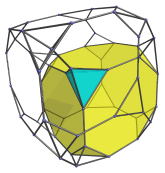
These truncated cubes are somewhat foreshortened because they are being viewed from an angle. In 4D, of course, they are perfectly uniform.
There are another 4 tetrahedra visible from this viewpoint besides the nearest tetrahedron:
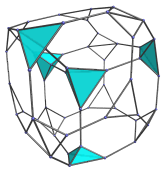
There are 6 pairs of triangular faces that lie on the projection envelope; these belong to 6 tetrahedra that lie on the far side of the projection, and so are not visible here. The pairs of triangular faces that are visible actually belong to the 4 truncated cubes we saw, but we show them in isolation below to indicate where those 6 hidden tetrahedra connect with the truncated cubes.

Finally, the last 4 triangular faces on the projection envelope are joined to 4 tetrahedra on the far side of the truncated tesseract that are in dual orientation to the 4 visible tetrahedra we saw. Again, they belong to the 4 truncated cubes, but we show them below to indicate where they lie on the far side:

They are surrounded by another 4 truncated cubes, also in dual orientation, which in turn surrounds the antipodal tetrahedron.
Animation
The following animation shows the truncated tesseract rotating in the XW plane.
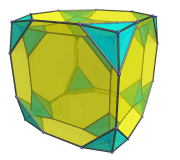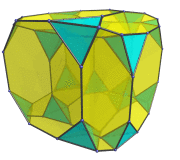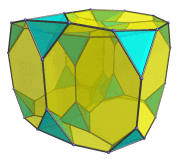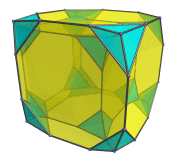
We turned off visibility clipping so that you can trace the full path of each cell as it rotates relative to the 4D viewpoint.
Coordinates
The coordinates of the truncated tesseract centered at the origin with edge length 2 are all permutations of coordinates and changes of sign of:
- (1, (1+√2), (1+√2), (1+√2))




