The Cantitruncated Tesseract
The cantitruncated tesseract is a uniform polytope in the tesseract family. Its surface consists of 56 cells (8 great rhombicuboctahedra, 32 triangular prisms, 16 truncated tetrahedra), 248 polygons (64 triangles, 96 squares 64 hexagons, 24 octagons), 384 edges, and 192 vertices.
The cantitruncated tesseract may be constructed by radially expanding the octagonal ridges of the truncated tesseract outwards, causing the truncated cubes to become great rhombicuboctahedra, the tetrahedra to become truncated tetrahedra, and creating 32 gaps which can be filled in by triangular prisms.
Structure
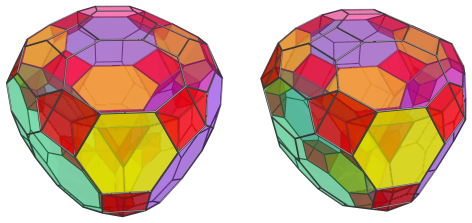
We shall explore the structure of the cantitruncated tesseract using its parallel projection into 3D, centered on a great rhombicuboctahedron:

This image shows the nearest cell to the 4D viewpoint. For clarity, we have omitted the edges that don't lie on this cell, and rendered the other cells in a light transparent color.
The 12 square faces of this nearest great rhombicuboctahedron are joined to 12 triangular prisms, shown in red below:
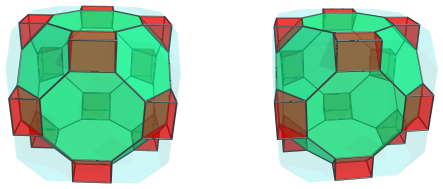
The hexagonal faces of the nearest cell are joined to 8 truncated tetrahedra:
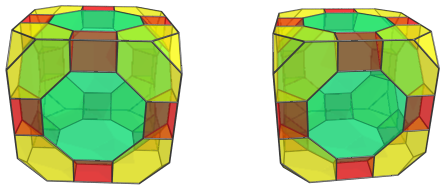
These are all the cells that lie on the near side of the cantitruncated tesseract. Past this point, we reach the cells on the “equator”:

These 8 triangles are actually the projection images of 8 triangular prisms that lie on the equator. They appear foreshortened into triangles because they are being seen from a 90° angle. In 4D, they are perfectly uniform triangular prisms.
For the sake of clarity, we have omitted the cells we saw previously.
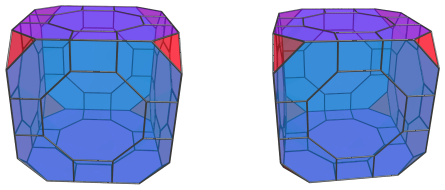
There are 6 other cells that lie on the equator, in 3 pairs:



These cells appear flattened into octagons, but that is only because they are being seen from a 90° angle. In 4D, they are perfectly uniform great rhombicuboctahedra.
Here are all of the equatorial cells together:
Past this point, we reach the far side of the cantitruncated tesseract, where the arrangement of cells exactly mirrors the arrangement on the near side, that we have seen previously.
In summary, the following table shows the cell counts in the various parts of the cantitruncated tesseract:
| Region | ||||
|---|---|---|---|---|
| Near side | 1 | 12 | 8 | |
| Equator | 6 | 8 | 0 | |
| Far side | 1 | 12 | 8 | |
| Total | 8 | 32 | 16 | |
| Grand total | 56 cells | |||
Coordinates
The Cartesian coordinates of the cantitruncated tesseract, centered on the origin and having edge length 2, are all permutations of coordinates and changes of sign of:
- (1, 1+√2, 1+2√2, 1+2√2)




