The Truncated 16-cell

---

The truncated 16-cell is a uniform polychoron bounded by 24 cells (16 truncated tetrahedra, 8 octahedra), 96 polygons (64 triangles, 32 hexagons), 120 edges, and 48 vertices.

The truncated 16-cell is the 4D analogue of the truncated octahedron.

• Just as the truncated octahedron may be constructed by truncating the 6 vertices of the octahedron, the truncated 16-cell may be constructed by truncating the 8 vertices of the 16-cell.

• Just as the truncation of the octahedron introduces 6 square faces, the truncation of the 16-cell introduces 8 octahedral cells.

• The truncation of the 16-cell causes its 16 tetrahedral cells to become truncated tetrahedra; similarly, the truncation of the octahedron causes its 8 triangular faces to become hexagons (truncated triangles).

• The envelope of the square-first parallel projection of the truncated octahedron is an octagon (truncated dual square); the envelope of the octahedron-first parallel projection of the truncated 16-cell is the truncated octahedron (truncated dual cube).

Structure

We shall explore the structure of the truncated 16-cell using its parallel projection into 3D, centered on an octahedral cell.

The above image shows the nearest octahedron to the 4D viewpoint, which projects to the center of the projection envelope.

Surrounding this octahedral cell are 8 truncated tetrahedra, shown below:

These cells appear to be distorted truncated tetrahedra; this is due to the foreshortening by the parallel projection. In 4D, they are perfectly uniform truncated tetrahedra. The following image shows all 8 of these cells together:

Together with the nearest octahedron, these 9 cells lie on the near side of the truncated 16-cell, its “equator”. The next layer of cells lie on the “equator” of the truncated 16-cell. These are shown next:

These 6 cells appear flattened as squares because they are seen at a 90° angle. In reality, they are perfectly regular octahedra.

After this, there are 8 more truncated tetrahedra on the “southern hemisphere” of the truncated 16-cell, in the same arrangement as above, followed by the farthest octahedral cell from the 4D viewpoint.

In summary, in the “northern hemisphere” there is 1 octahedron and 8 truncated tetrahedra; at the equator there are 6 octahedra; and in the “southern hemisphere” there are 8 truncated tetrahedra and 1 octahedron. In total, there are 8 octahedra and 16 truncated tetrahedra.

Animation

The following animation shows the perspective projection of the truncated 16-cell rotating in the XW plane.

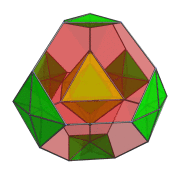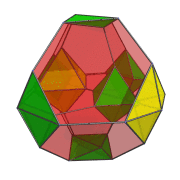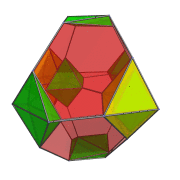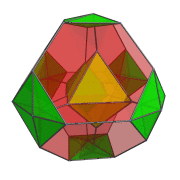
Octahedra that lie on the far side of the truncated 16-cell are rendered in green, and octahedra that lie on the near side in yellow. You can see the octahedra transition from green to yellow on the right side of the projection image as they rotate from the far side around to the near side.

Four of the green octahedra are rotating in-place—they lie on the YZ plane, stationary plane of the rotation. Another, independent, rotation is possible in this stationary plane. The following animation shows the truncated 16-cell undergoing this double-rotation:

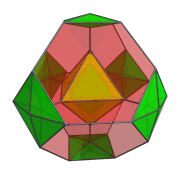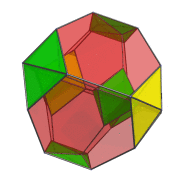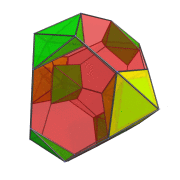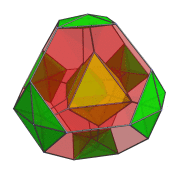
In this animation, you can see how the 4 octahedra in the YZ plane are both rotating in-place and in the YZ plane. Similarly, the other 4 octahedra are rotating in the XW plane while simultaneously undergoing a spinning motion: rotation in the YZ plane.

Coordinates

The Cartesian coordinates for the truncated 16-cell, centered on the origin and having edge length 2, are all permutations of coordinates and changes of sign of:

• (0, 0, √2, 2√2)