The 600-Cell

---

The 600-cell is composed of 600 tetrahedra, joined 5 to an edge. It has 120 vertices, 720 edges, and 1200 triangles; and is the dual of the 120-cell.

It is the 4D equivalent of the icosahedron, just as the 120-cell is the 4D equivalent of the dodecahedron. Its vertex figure is an icosahedron. Twenty tetrahedral cells meet at every vertex, in an icosahedral arrangement. The faces of these tetrahedra opposite the central vertex form the faces of an icosahedron.

Structure

We will explore the 600-cell using two projections: its vertex-first parallel projection, and a side view that helps us track our progress. We begin with the nearest vertex to the 4D viewpoint, shown in the first image below.

The nearest vertex is shown here in red, and lies at the center of the projection envelope in the first image. For the sake of clarity, we render all cells in a light transparent color and omit all edges and vertices except this nearest vertex. We may regard it as the “north pole” of the 600-cell. For comparison, the second image shows the 600-cell viewed from the side, with this north pole vertex on top.

Surrounding this central vertex are 20 tetrahedral cells in an icosahedral arrangement. The next two images show these 20 cells:

The icosahedral arrangement of these cells is obvious in the first image. These cells may be thought of as the “arctic circle” cells, surrounding the north pole, as illustrated by the side view shown in the second image. The faces of the icosahedron are the “southernmost” faces of each tetrahedron. In the second image, this icosahedron projects to a flat plane making it clear that the apices of the 20 tetrahedra meet at the north pole vertex above the hyperplane containing the icosahedron. The faces of this icosahedron are joined to another 20 cells, shown in the next images:

It is obvious that between each adjacent pair of these cells is a gap where another tetrahedron may fit into. Each of these gaps corresponds with an edge in the previous icosahedral complex, so there are 30 gaps in total, into which 30 other tetrahedra may fit, as shown in the next images:

The boundary of these cells now form a dodecahedron with pentagonal depressions in each face. A circle of 5 tetrahedra sharing an edge can fit into each of these depressions, for a total of 60 more tetrahedra. The following images show these tetrahedra fitted in.

Each circle of 5 tetrahedra touch a single vertex in the original icosahedral complex in the first layer of cells. Hence, these circles correspond with the vertices of the icosahedron.

The boundary of these cells now form a pentakis dodecahedron (a dodecahedron with pentagonal pyramids erected on each of its faces) in the vertex-first projection. Each of its faces connects to yet another tetrahedron, for a total of another 60 tetrahedra. The following images show these tetrahedra attached:

There are shallow indentations in the cells shown above, where more tetrahedra can fit into. The following images show 60 more tetrahedra filled in:

There are 20 more gaps into which more tetrahedra may fit. We now fill those in as well:

These 20 cells lie at the same “latitude” as the other cells, so the side view in the second image is almost identical to the previous side view.

Now we are at the “equator” of the 600-cell, the midpoint between the north pole vertex and the south pole vertex. The following images show the cells that lie on the equator. For clarity, we have omitted the other cells we have seen thus far.

There are 60 equatorial cells, consisting of 12 circles of 5 tetrahedra each. Each circle of tetrahedra shares an edge. They appear completely flattened in the first image because they are at a 90° angle from the 4D viewpoint. The edge shared by each circle of tetrahedra has also been projected to a point because of the angle with the viewpoint. The second image shows that these are circles of regular tetrahedra surrounding an edge each.

After these equatorial cells, the layers we have seen so far repeat themselves in reverse, this time on the far side of the 600-cell, until we reach the single vertex at the south pole.

In summary, we have 20 cells in an icosahedral arrangement in the first layer, 20 cells sharing a face with that icosahedron, 30 cells sharing an edge with the icosahedron. Together, these have a boundary in the shape of a dodecahedron with pentagonal depressions. There are 60 cells sharing a vertex with the icosahedron, filling in these depressions and thereby augmenting this dodecahedron into a pentakis dodecahedron. Then there are 60 cells sharing a face with the pentakis dodecahedron, 60 cells (in 30 pairs) sharing an edge with the original dodecahedron, and 20 cells sharing a vertex with the original dodecahedron. These form a total of 270 cells in the northern hemisphere of the 600-cell. The southern hemisphere exactly mirrors the same arrangement of cells, giving a total of 540 cells. Finally, the 60 equatorial cells bring the final total to 600 cells.

Other Projections

Perspective Projection

The following image shows the perspective projection of the 600-cell into 3D:

This time, the viewpoint is centered on one of the tetrahedral cells, which is shown above in dark blue. The cells sharing a face with this cell are shown in cyan, while the cells sharing an edge with it are shown in green. The cells in yellow share a vertex with this cell, and the remaining cells are in red. Cells on the far side of the 600-cell have been culled for clarity.

Embedded Icosahedral Polyhedra

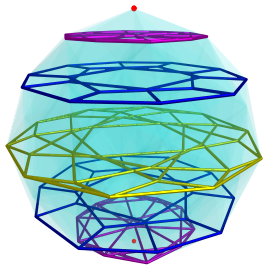
The following image shows the various polyhedra from the icosahedron family that occur as subsets of the edges in the 600-cell:

The nearest vertex is shown in red, at the center of the image. The first layer of cells shows an icosahedral boundary (magenta). The next layer, consisting of cells that share faces and edges with the first layer, has a dodecahedral boundary (blue). Then the third layer of cells shows an embedded icosidodecahedron (yellow), which lies on the equator of the 600-cell. After this, in the southern hemisphere, there is another embedded dodecahedron, then an icosahedron, and then the south pole vertex, each of which coincides in projection with its counterpart in the northern hemisphere. The following image shows the side-view of these polyhedra, including the ones embedded in the southern hemisphere:

Coordinates

The coordinates of the 600-cell are all permutations of coordinates and changes of sign of:

(1,1,1,1)
(2,0,0,0)

and all even permutations and all changes of sign of:

(φ,1,φ⁻¹,0)

where φ=(1+√5)/2 is the Golden Ratio.

These coordinates give an origin-centered 600-cell with edge length 2/φ.

Related polychora

The 600-cell is related to two other polychora in an interesting way.

A 24-cell can be inscribed in a 600-cell, and if the vertices that coincide with the 24-cell's vertices are removed, then the convex hull of the remaining vertices forms the snub 24-cell, an interesting semi-regular polychoron with icosahedral and tetrahedral cells.

Two mutually orthogonal rings of vertices can also be removed from the 600-cell. The convex hull of the remaining vertices is the grand antiprism.