4D Visualization
Interpreting 4D Projections (2)
Inferring 4D Depth
We now take a closer look at how to infer 4D depth from a 3D projection. We have actually already indicated how this is done in the previous chapters; now we make it explicit.
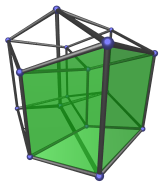
Look at the “cube-within-a-cube” projection of the hypercube again:
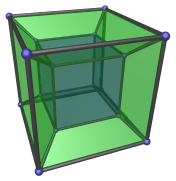
We've said in chapter 9 that the blue cube is farther away from the viewer than the outer cube, which is why it appears to be smaller. In other words, when something appears to be smaller than normal, it's an indication that it's farther away in the 4th direction.
We now take a closer look at this matter.
A Fresh Look at the Hypercube
Let's look at the same hypercube again from a slightly different angle.
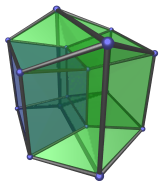
Don't be surprised by the odd appearance of this projection; this is still the same hypercube we're looking at. We've only shifted our viewpoint a little. Now we are looking at the right square face of the blue cube that it shares with the frustum on the right.
Notice how the blue cube is now also a frustum, and its neighbour on the right is now a slightly-elongated frustum. What's happening here? The left square face of the blue cube is now larger than its right square face. Remember what we just said about size implying 4D distance? In particular, relative sizes imply relative distance. The fact that the left square face is larger than the right square face means that it is closer to our 4D viewpoint than the right face. For one face of the blue cube to be closer than the other face means that the blue cube is now at an angle from our viewpoint.
Compare this situation with the analogous 3D situation below:


Notice how the blue square, when seen from an angle, appears as a trapezium with its left edge longer than its right edge? It is exactly the same situation in the 4D case:


Can you see the analogy?
The Nearest Ridge
Let's see how we are confident in inferring 4D depth. What is closest to the 4D viewpoint in the right image? Can you guess?
The answer is, the square face that bisects the image, shown in red below on the right. To help you understand why this is so, the left image shows the analogous situation in 3D, with the nearest edge colored in red:


Due to the number of faces present in the 4D projection, we've increased the transparency of the green faces so that the red face shows up better. Notice how it projects to the center of the image.
As you can see by dimensional analogy, in the 4D case everything has gone up by one dimension. In 3D, the nearest edge (a 1D line segment) is where two faces (2D squares) meet. The projection envelope is a hexagon (a 2D area). In 4D, the nearest face (a 2D square) is where two cells (3D cubes) meet. The projection envelope is a square bifrustum (a 3D volume).
The Farthest Ridge
What about the farthest ridge?
In the 3D case, the farthest edge is obviously the short edge behind the red edge, obscured by it because we used a non-transparent color for the red edge. We temporarily hide the nearest edge in the next image, and color the farthest edge red, in order to show it clearly:

The 4D case is shown below. We also hide the nearest ridge, because the farthest ridge is coplanar with it in the projection and would obscure it.
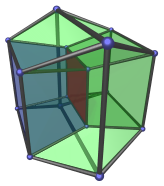
This should be simple to understand.
Notice how this farthest ridge also projects to the center of the projection image, just like the nearest ridge. It is interesting that both the nearest and farthest features of the hypercube project to the center of the image. While this is not necessarily true for 4D objects in general, it is true for convex objects. We shall revisit this point later when we discuss the visualization of convex 4D polytopes.
What Comes Between
Now let's look at a slightly more tricky part of the 4D projection, the two cells shown below:
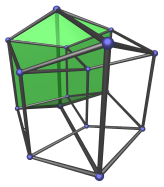
It may not be immediately obvious which part of the 3D cube these two cells are analogous with. While we could, by a round-about rationalization of the situation, draw an analogy with the top and bottom faces of the 3D cube, such dimensional analogy is not very insightful in this case. Instead, we should simply accept that these two cells are a new phenomenon that in 4D, and study them by way of inferring 4D depth.
First of all, it should be clear that these two cells are really perfectly regular cubes in 4D. They only appear in their peculiar shapes because they are being projected from an angle.
Each of them share a vertical edge with the nearest ridge, and opposite the shared edge is a much shorter vertical edge shared with the farthest ridge. From what we've learned of depth inference, we realize that these two cells are on the “side” of the hypercube, joining the nearest ridge to the farthest ridge.
Their two other vertical edges have intermediate lengths, between that of their longest and shortest edges. This progression of edge lengths is caused by the gradual foreshortening of these cubes as they extend farther away into 4D. The decreasing edge lengths serve as 4D depth markers, telling us which way each cube is “slanting” into the 4th direction.

