The 3,4-Duoprism

---

The 3,4-duoprism is a 4D uniform polychoron in the infinite duoprism family. It is the Cartesian product of a triangle and a square, and is bounded by 4 triangular prisms and 3 cubes.

This is the perspective projection of the 3,4-duoprism into 3D, centered on one of its square ridges.

Triangular prism-prism

The 3,4-duoprism is the same as the extruded triangular prism, that is, the prism of a triangular prism. This construction of the 3,4-duoprism is more readily seen from a different 4D viewpoint:

With this “triangular prism within a triangular prism” projection, it is easier to see how the 3,4-duoprism is formed by extruding a triangular prism. The outer and inner triangular prisms may be regarded as the endpoints of the extrusion. Starting from the outer prism, as we extrude it towards the inner prism, its triangular caps trace out 2 more triangular prisms, and its square faces trace out cubes (seen here as flattened frustums due to foreshortening).

Structure

The 4 triangular prism cells of the 3,4-duoprism form a ring, as shown by the images below:

The 3 cubical cells of the 3,4-duoprism also form a ring, shown next:

Most of these cells have been foreshortened by perspective projection, causing them to appear squished or otherwise deformed. However, this is only because they are seen at an angle; in 4D, they are perfectly uniform triangular prisms and perfectly regular cubes.

Animations

The following animation shows the 3,4-duoprism rotating in the plane of the ring of 3 cubes:

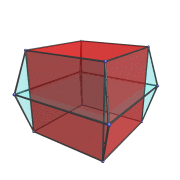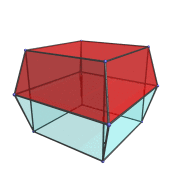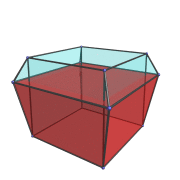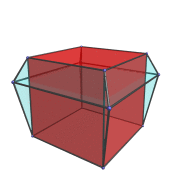
We've rendered one of the cells in red and everything else in a transparent color, so that you can see the path traced out by the cell as it rotates.

The next animation shows the 3,4-duoprism doing a double rotation in both the plane of its 3 cubes and also in the plane of its 4 triangular prisms.

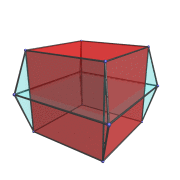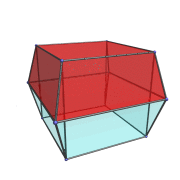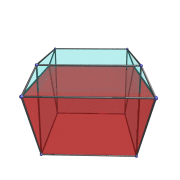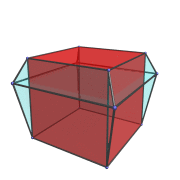
This composite rotation, possible only in 4D and above, is composed of a simple rotation in the plane of the cubes and another simple rotation in the plane of the triangular prisms at 1/4 the rotation rate of the former. Notice how the vertices of the 3,4-duoprism trace out spiralling paths characteristic of these complex gyrations.