4D Visualization
Cross-sections
Using Cross-sections
Since we are creatures confined to 3D, we have no way of directly exploring higher-dimensional objects. We can, however, employ various indirect means to study and understand them. One method is to intersect a higher-dimensional object with our world to see what its various cross-sections look like.
To illustrate this, let's apply dimensional analogy again. Suppose we are only 2D beings, living in a 2D world, and unable to see into the 3rd dimension. Suppose we're trying to understand what a cylinder is. We know what circles and squares are, because these objects exist in our 2D world and we can directly handle and see them. But we haven't the slightest idea what a cylinder might be. We have no way of directly seeing such an object, because our retina is only 1D, and a 2D retina is needed to adequately perceive a 3D object. What we can do, is to examine what happens when a cylinder passes through our 2D world:
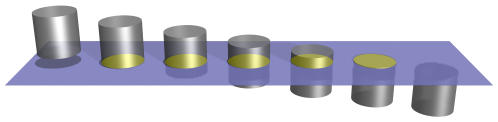
As the cylinder does this, we can observe its cross-sections with our planar world. For example, if the cylinder descends through our world vertically, we would see a series of circular cross-sections, all of a constant size.

Now, as we have mentioned in the previous chapter, 2D beings cannot actually see the above image directly; they can only see the circular cross-sections from the side. The cross-sections will appear as line segments that show curvature from the way they interact with nearby light sources. Nevertheless, it is reasonable to assume that, as diligent 2D beings trying to understand 3D, we will, through careful study of these cross-sections from various angles, eventually form a mental model of these cross-sections that more-or-less corresponds with what is depicted above. For the sake of conciseness, we will continue to present these 2D images as they would appear from 3D; however, it is to be understood in each case that 2D beings can only imagine such diagrams in their mind after careful study.
In any case, from these circular cross-sections, we may conclude that the cylinder must be something circular.
We can also observe the cylinder passing through our world in a different orientation:

This time, the cylinder passes through round-side first. What we see is a series of rectangular cross-sections that seem to grow and shrink in length but remain constant in width. From this, we conclude that the cylinder must have something rectangular about it.

Thus far, we learned that a 3D cylinder is something that is both circular and rectangular. This is obviously correct. Examining cross-sections has yielded valuable information about the shape of a cylinder.
A Fundamental Weakness
Now, still supposing we are only 2D creatures, we have a hard time understanding how something can be both circular and rectangular at the same time, as we've just learned. As 2D creatures, we only have experience with 2D shapes, and none of them are simultaneously a circle and a rectangle. We may try to investigate this further by observing the cylinder pass through our 2D world at a 45-degree angle:

The cross-sections are now rather puzzling:

They consist not of regular circles or rectangles but of ellipses in various states of truncation. Unless we knew beforehand, we would probably not be able to deduce the shape of a cylinder from these cross-sections. We may even think that these are cross-sections of a different object altogether.
This illustrates a fundamental weakness of the cross-sections method: although it does yield some useful information, it is difficult to synthesize this information into a coherent model of the actual object. For example, if we only knew the above sequence of cross-sections of the cylinder, it would be rather hard for us to deduce that a cylinder has two circular lids and a curved side.
The following sequence of cross-sections further illustrate this weakness:

Can you guess what 3D object would produce this sequence of cross-sections?
Probably not, unless you knew it beforehand.
These are, in fact, cross-sections of the 3D cube, which are produced when the cube passes through the 2D world corner-first. It is rather difficult to know this just by examining these cross-sections alone; information about the object such as the number of vertices (corners) and the number and shape of its faces are not readily apparent. Most people probably don't even know that a cube can make a hexagonal cross-section with a plane!
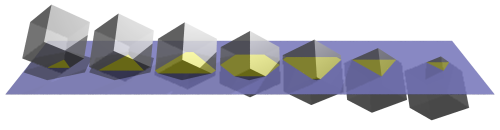
Now, as 3D beings, we at least have some knowledge of 3D geometry to be able to imagine the cross-sections stacked on top of each other, and perhaps deduce a vaguely cube-like shape from them. But consider the following sequence of cross-sections of a 4D object with 3D space:

Can you figure out what the 4D object is?
Likely not, unless you knew it beforehand, since you would have a hard time understanding just how these cross-sections could fit together. Without an intuitive grasp of 4D, it is very hard to reconstruct the original object from them.
The fundamental problem with cross-sections is that we are examining the object piecemeal. Important features such as the number and shape of facets, the number of vertices (corners), and the overall shape of the object, are only implied, not explicit.
A better approach is to use projections, as we will discuss in the next chapter.

