The Dodecahedron
The regular dodecahedron is a Platonic solid bounded by 12 regular pentagons. It has 20 vertices and 30 edges.

The dual of the dodecahedron is the icosahedron. The dodecahedron occurs as cells in the 120-cell and the runcinated 120-cell.
A dodecahedron can be augmented by a pentagonal pyramid to produce an augmented dodecahedron (J58), one of the Johnson solids. Adding a second pentagonal pyramid on the opposite side produces the parabiaugmented dodecahedron (J59). If the second pyramid is attached to a face an edge away from the first pyramid, the metabiaugmented dodecahedron (J60) is produced instead.
Three augments can be added if they are placed on three mutually non-adjacent pentagons. The result is the triaugmented dodecahedron (J61).
Projections
In order to be able to identify the dodecahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:
| Projection | Envelope | Description |
|---|---|---|
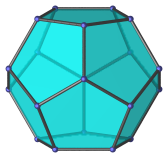 |
Non-regular dodecagon | Vertex-first parallel projection. |
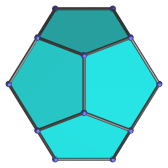 |
Non-regular hexagon | Edge-first parallel projection. Four of the dodecahedron's faces project onto 4 of the edges of the hexagonal envelope. |
 |
Regular decagon | Face-first parallel projection. |
 |
Non-regular octagon | Parallel projection parallel to top and bottom faces. The top and bottom faces project to the top and bottom edges of the projection envelope. |
Coordinates
The Cartesian coordinates for the regular dodecahedron, centered on the origin with edge length 2, are:
- (±φ, ±φ, ±φ)
- (0, ±φ2, ±1)
- (±φ2, ±1, 0)
- (±1, 0, ±φ2)
where φ=(1+√5)/2 is the Golden Ratio.




