The Pentagonal Pyramid
The pentagonal pyramid is one of the Johnson solids. It is bounded by 5 equilateral triangles and 1 pentagon, for a total of 6 faces, 10 edges, and 6 vertices. It is the second polyhedron in Norman Johnson's list, and thus bears the label J2.
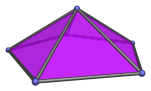
A pentagonal pyramid of edge length 2 has height √((10−2√5)/5), or approximately 1.05146. It is therefore quite a shallow pyramid, barely over half of its edge length. In 4D, this fact causes the pentagonal prism pyramid, which has two pentagonal pyramid cells, to be very shallow indeed. This in turn has the consequence that a very large number of 5,n-duoprisms, up to n=20, can be augmented with pentagonal prism pyramids and remain convex, thus producing a large number of CRF augmented duoprisms: 1578 distinct augmentations just from the 5,n-duoprisms alone.
Two pentagonal pyramids can be attached to each other to form the pentagonal bipyramid (J13).
A pentagonal pyramid can be attached to a dodecahedron to form an augmented dodecahedron (J58). Adding a second pentagonal pyramid on the opposite side produces the parabiaugmented dodecahedron (J59). If the second pyramid is added on a non-adjacent, non-opposite face, the result is the metabiaugmented dodecahedron (J60). The latter can support a third augment on a face non-adjacent to the first two augments, resulting in the triaugmented dodecahedron (J61).
Projections
In order to be able to identify the pentagonal pyramid in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:
| Projection | Envelope | Description |
|---|---|---|
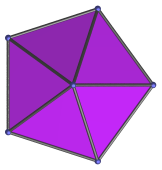 |
Pentagon | Top view (apex-centered parallel projection). |
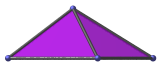 |
Scalene triangle | Projection parallel to pentagonal base. One of the triangular faces projects to the upper left edge. |
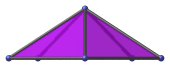 |
Isosceles triangle | Projection parallel to pentagonal base, with reflective symmetry. |
Coordinates
The simplest Cartesian coordinates of the pentagonal pyramid can be obtained from the regular icosahedron, since the icosahedron can be cut into a pentagonal antiprism and two pentagonal pyramids. This derivation of the pentagonal antiprism yields the following coordinates:
- (0, ±1, φ)
- (±1, φ, 0)
- (±φ, 0, 1)
where φ=(1+√5)/2 is the Golden Ratio.
These coordinates are algebraically “nice”, in that everything can be neatly expressed in terms of the Golden Ratio. However, the pentagonal pyramid produced by these coordinates is not origin-centered and not in a “nice” orientation. If we start instead from the coordinates of the regular pentagon and erect a pyramid over it, we obtain the following origin-centered coordinates that yield an ”upright“ pentagonal pyramid:
- (√((10+2√5)/5), 0, −√((5−√5)/90))
- (√((5−√5)/10), ±φ, −√((5−√5)/90))
- (−√((5+2√5)/5), ±1, −√((5−√5)/90))
- (0, 0, √(5*(5−√5)/18))
The pentagonal pyramid yielded by these coordinates has edge length 2.
Occurrences
The pentagonal pyramid occurs as cells in the following 4D polytopes:




