The Metabidiminished Icosahedron
The metabidiminished icosahedron is one of the Johnson solids. It is bounded by 10 regular triangles and 2 regular pentagons, for a total of 12 faces, 20 edges, and 10 vertices. It may be constructed by removing 2 vertices from the regular icosahedron such that 2 adjacent pentagonal faces are formed. It is the 62nd polyhedron in Norman Johnson's list, and thus bears the label J62.
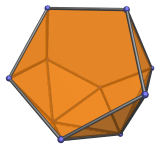
Removing two vertices from the icosahedron causes a reduction in its symmetry, so the metabidiminished icosahedron only has a two-fold axis of symmetry around the edge shared by the two pentagons, extending to the opposite edge. The angle between the two pentagons is acos(1/√5) ≈ 63.43°, giving it a wedge-like shape. We may thus group its triangular faces into several equivalence classes:
Two wedge triangles that sit between the two pentagons;
Two lateral triangles that connect the wedge triangles to the edge opposite the edge between the two pentagons;
Two back triangles that share this opposite edge;
Four oblique triangles between the pentagons, lateral triangles, and back triangles.
Projections
In order to be able to identify the metabidiminished icosahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:
| Projection | Envelope | Description |
|---|---|---|
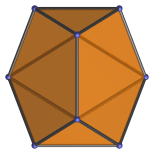 |
Hexagon | Parallel projection along axis of symmetry. Coincides with the edge-first projection of the icosahedron. The wedge and lateral triangles coincide in this projection. |
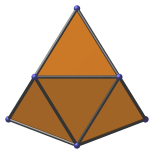 |
Inverted kite | Parallel projection parallel to top and bottom edges. The long edges of the kite are the images of the pentagons. |
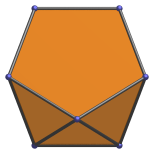 |
Hexagon | Parallel projection perpendicular to top and bottom edges. |
Coordinates
The Cartesian coordinates of the metabidiminished icosahedron are:
- (±1, ±φ, 0)
- (±φ, 0, ±1)
- (0, −1, ±φ)
where φ=(1+√5)/2 is the Golden Ratio.
These coordinates are obtained by deleting 2 vertices from the regular icosahedron such that 2 adjacent pentagonal faces are formed.
Occurrences
The metabidiminished icosahedron appears as cells in many CRF polychora, generalizations of the Johnson solids to 4D, especially those related to the 600-cell family of uniform polychora. Its wedge-like shape serves as a convenient interface between cells having pentagonal faces in many CRF constructions. Its occurrences include (but are not limited to) the following polytopes:




