The Disphenocingulum

---

The disphenocingulum is the 90th Johnson solid (J90). Its surface consists of 24 faces (20 equilateral triangles and 4 squares), 38 edges, and 16 vertices.

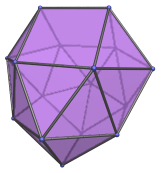
The disphenocingulum is one of the special Johnson solids at the end of Norman Johnson's list that are not directly derived from the uniform polyhedra by cut-and-paste operations. As Norman Johnson explains, a lune is a square with two opposite edges attached to equilateral triangles, and a spheno (Latin for wedge) complex is two lunes joined together to form a wedge-like structure. The prefix di- means two, and cingulum (Latin for belt) refers to a belt of 12 triangles. Thus, di-spheno-cingulum refers to taking two spheno complexes and joining them to either side of the belt of 12 triangles. It so happens that if the spheno complexes are rotated 90° with respect to each other, the result can be closed up into a polyhedron with regular faces.

Projections

Here are some views of the disphenocingulum from various angles:

Projection	Description
	Top view.
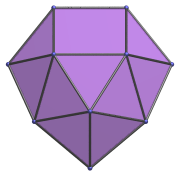	Front view.
	45° side view.

Coordinates

The Cartesian coordinates of the disphenocingulum, centered on the origin with edge length 2, are:

• (±1, 0, A)
• (±1, ±B, C)
• (±D, 0, E)
• (0, ±D, −E)
• (±B, ±1, −C)
• (0, ±1, −A)

where B is the root of the following polynomial between 1.5 and 1.6:

B¹² − 4B¹¹ − 26B¹⁰ + 116B⁹ + 97B⁸ − 824B⁷ + 312B⁶ + 2176B⁵ − 2024B⁴ − 1888B³ + 2688B² − 192B − 368 = 0

and:

C	=	√((1+2B−B2) / 2)
A	=	C + √(4−B2)
E	=	(A2−B2−C2) / (2√(4−B2))
D	=	1 + √(4−(A−E)2)

Numerically, A, B, C, D, and E have the approximate values:

• A = 2.208875884159868
• B = 1.534262227966923
• C = 0.925895207830730
• D = 2.252966294157959
• E = 0.650005951899941