The Gyroelongated Pentagonal Rotunda
The gyroelongated pentagonal rotunda is the 25th Johnson solid (J25). It has 30 vertices, 65 edges, and 37 faces (30 equilateral triangles, 6 pentagons, and 1 decagon).

The gyroelongated pentagonal rotunda can be constructed by attaching a decagonal antiprism to a pentagonal rotunda (J6), thereby lengthening it. The gyro in the name refers to how the bottom decagonal face is gyrated with respect to the decagonal face of the constituent rotunda.
J25 can be augmented with a pentagonal cupola to produce the gyroelongated pentagonal cupolarotunda (J47). Adding another rotunda produces the gyroelongated pentagonal birotunda (J48).
Projections
Here are some views of the gyroelongated pentagonal rotunda from various angles:
| Projection | Description |
|---|---|
 |
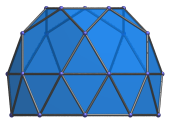
Top view. |
 |
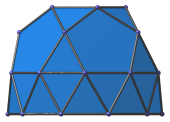
Front view. |
 |
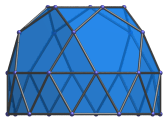
Side view, with many coincident edges. |
 |
9° side view, with rectangular image of antiprism. |
Coordinates
The Cartesian coordinates of the gyroelongated pentagonal rotunda with edge length 2 are:
- (0, −√((10+2√5)/5), √((20+8√5)/5))
- (±1, √((5+2√5)/5), √((20+8√5)/5))
- (±φ, −√((5−√5)/10), √((20+8√5)/5))
- (0, √((20+8√5)/5), √((10+2√5)/5))
- (±φ, −√((25+11√5)/10), √((10+2√5)/5))
- (±φ2, √((5+√5)/10), √((10+2√5)/5))
- (±1, ±√(3+4φ), 0)
- (±φ2, ±√(2+φ), 0)
- (±2φ, 0, 0)
- (0, ±2φ, −2√(√(11φ+7)−2φ−1))
- (±√(3+4φ), ±1, −2√(√(11φ+7)−2φ−1))
- (±√(2+φ), ±φ2, −2√(√(11φ+7)−2φ−1))
where φ = (1+√5)/2 is the Golden Ratio.




