The Elongated Triangular Orthobicupola
The elongated triangular orthobicupola is the 35th Johnson solid (J35). It has 18 vertices, 36 edges, and 20 faces (8 equilateral triangles and 12 squares).
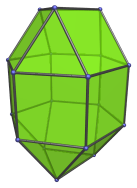
The elongated triangular orthobicupola can be constructed by attaching two triangular cupolae to a hexagonal prism. Equivalently, it can be constructed by inserting a hexagonal prism between the two constituent cupolae of the triangular orthobicupola (J27). The ortho- in the name refers to how the orientation of the top and bottom triangles are aligned with each other. If the top and bottom triangles are rotated with respect to each other, the elongated triangular gyrobicupola (J36) is produced instead.
Projections
Here are some views of the elongated triangular orthobicupola from various angles:
| Projection | Description |
|---|---|
 |
Top view. |
 |
Front view. |
 |
Side view. |
Coordinates
The Cartesian coordinates of the elongated triangular orthobicupola with edge length 2 are:
- (±1, −1/√3, ±(1+√(8/3)))
- (0, 2/√3, ±(1+√(8/3)))
- (±1, ±√3, ±1)
- (±2, 0, ±1)




