The Gyrate Bidiminished Rhombicosidodecahedron

---

The gyrate bidiminished rhombicosidodecahedron (J82) is the 82nd Johnson solid. It has 50 vertices, 90 edges, and 42 faces (10 triangles, 20 squares, 10 pentagons, 2 decagons).

It is constructed by removing 2 pentagonal cupolae from the rhombicosidodecahedron such that 2 non-parallel decagonal faces are formed, and gyrating one of the remaining pentagonal cupola segments that were not truncated by the diminishing, so that its square faces line with adjacent square faces.

Equivalently, J82 can be constructed from J81 (metabidiminished rhombicosidodecahedron) by gyrating one of the J81's pentagonal cupola segments.

The difference between J81 and J82 may not be immediately obvious, but J82 may be identified by the 5 tell-tale pairs of squares sharing an edge where the gyrated pentagonal cupola meets the rest of the rhombicosidodecahedral part of J82's surface. The following image shows these pairs highlighted in green:

J81 does not have such pairs of adjacent square faces, but J82 does. They only occur on one side of the J82; the other side has the usual arrangement of squares alternating with triangles.

The next image highlights the gyrated pentagonal cupola segment:

Due to the non-equivalence of its vertices, the gyrate bidiminished rhombicosidodecahedron only has a single plane of symmetry: a 2-fold symmetry around the plane that bisects it.

Projections

Here are some views of the gyrate bidiminished rhombicosidodecahedron from various angles:

Projection	Description
	Top view, centered on square between decagons.
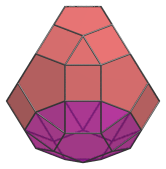	Front view, showing its wedge-like shape.
	Side view.

Coordinates

The Cartesian coordinates for the gyrate bidiminished rhombicosidodecahedron with edge length 2 are:

• (±1, ±1, φ³)
• (±φ, ±φ², 2φ)
• (0, ±(2+φ), φ²)
• (±φ², ±2φ, φ)
• (±1, ±(2φ+1), 1)
• (±(φ+2), ±φ², 0)
• (±1, ±(2φ+1), −1)
• (±(2φ+1), ±1, −1)
• (±φ², ±2φ, −φ)
• (±2φ, ±φ, −φ²)
• (0, (2+φ), −φ²)
• (±φ², 0, −(φ+2))
• (±φ, φ², −2φ)
• (±1, 1, −φ³)

• (±1, −(6φ+7)/5, −(8φ+1)/5)
• (±φ, −(7+φ)/5, −(8φ+6)/5)
• (0, −(φ+2)/5, −(13φ+1)/5)

where φ=(1+√5)/2 is the Golden Ratio.