The Elongated Square Gyrobicupola
The elongated square gyrobicupola is the 37th Johnson solid (hence, the moniker J37), having 18 square faces and 8 triangular faces, for a total of 26 faces, 48 edges, and 24 vertices.

It is also known as the gyrate rhombicuboctahedron, or pseudo-rhombicuboctahedron, because it has exactly the same faces as the rhombicuboctahedron and the same configuration of faces (3 squares and a triangle) around each vertex, but is not uniform because its vertices are not transitive. It may be thought of as a rhombicuboctahedron, treated as an elongated square bicupola, in which a square cupola is rotated by 45°.
Due to the non-transitivity of its vertices, the elongated square gyrobicupola only has one axis of symmetry, passing through the two opposite square faces that are rotated 45° relative to each other.
Projections
In order to be able to identify J37 in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:
| Projection | Description |
|---|---|
 |
Projection parallel to axis of symmetry. |
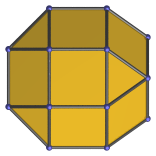 |
Projection perpendicular to axis of symmetry. |
 |
Oblique view. |
Coordinates
The Cartesian coordinates of the elongated square gyrobicupola, centered on the origin and with edge length 2, are:
- (1+√2, 0, ±√2)
- (1+√2, ±√2, 0)
- (±1, ±1, ±(1+√2))
- (±1, ±(1+√2), ±1)
- (−(1+√2), ±1, ±1)
These coordinates are obtained from the rhombicuboctahedron by replacing the 4 vertices of an axial square face with the 4 vertices of a rotated square.
Occurrences
The elongated square gyrobicupola occurs as cells in the following 4D polytopes:




