The Biparabigyrated Cantellated Tesseract
The biparabigyrated cantellated tesseract is a CRF polychoron bounded by 68 cells (8 elongated square gyrobicupolae (J37), 24 square pyramids, 32 triangular prisms, 4 octahedra), 260 polygons (128 triangles, 132 squares), 288 edges, and 96 vertices. It is an interesting CRF polychoron that substitutes J37's for the rhombicuboctahedral cells in the cantellated tesseract, and can be constructed from the latter by gyrating four square magnabicupolic ring segments, in analogy to the derivation of J37 from the rhombicuboctahedron by gyrating one of its square cupola segments. As such, it may be termed the pseudo-cantellated tesseract.
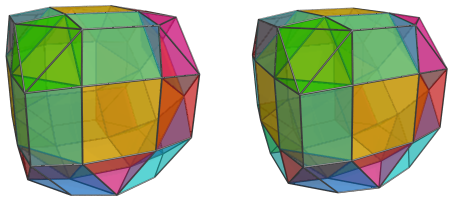
Construction
The biparabigyrated cantellated tesseract may be constructed by replacing the vertices of 4 square ridges in the cantellated tesseract with the vertices of the same squares rotated by 45°. This process causes a number of octahedral cells to break up into square pyramids, and turns the rhombicuboctahedra into gyrate rhombicuboctahedra, that is, J37's.
Alternatively, it may be constructed by augmenting an 8,8-duoprism with two rings of 4 suitably-oriented square magnabicupolic rings. This construction leads to an alternative name, biparabigyroaugmented 8,8-duoprism.
Structure
In spite of its irregularity, the biparabigyrated cantellated tesseract follows the structure of the uniform cantellated tesseract pretty closely. We shall explore this structure by using its parallel projections into 3D.
The Near Side
The above image shows the nearest J37 to the 4D viewpoint. For clarity, we have omitted edges and vertices on all other cells, and rendered the other cells in a light transparent color.
On the left side, touching the nearest J37's triangular faces, are two octahedra in the same places as in the cantellated tesseract:
The other two triangular faces on the left side are joined to two square pyramids:
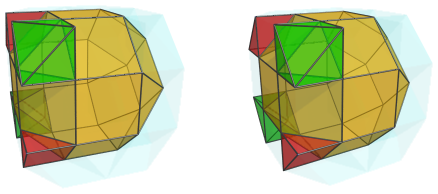
If you compare this with the projections of the cantellated tesseract, you can see that these square pyramids sit where two more octahedra sit in the cantellated tesseract. So, they may be thought of as the remnants of those octahedra, with their bottom halves sliced off by the gyration that produced this polychoron.
This slicing of octahedra into square pyramids can be clearly seen on the right side of the projection, where the gyrated square cupola portion of the nearest J37 is. Hanging off two of the edges of the J37 are two more square pyramids:
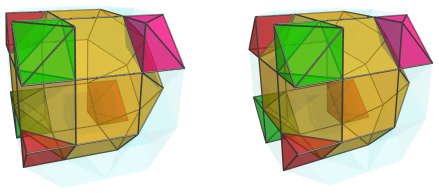
These square pyramids are, again, where two octahedra lie in the cantellated tesseract; but here they have been sliced in half by the gyration that rotated the right portion of the J37 into place.
The two remaining corners have an even more interesting twist: not only have the octahedra that were there been sliced into two square pyramids, but both parts have been rotated away from their original positions by the gyrations that produced this CRF polytope. So, instead of square pyramids or octahedra, four triangular prisms sit in those positions, in two pairs:
The triangular prisms are joined to each other base to base, but due to the slight dichoral angle between them, they are not coplanar, and so do not form gyrobifastigiums (J26). The square pyramids, though, if they were rotated back to their original positions, would be coplanar with each other, and form the original octahedra in the cantellated tesseract.
Of course, the square pyramids are also paired up with triangular prisms by the gyration:
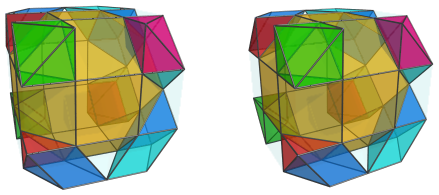
Here, we see the correspondence between the cantellated tesseract's octahedra and various pairings of square pyramids and triangular prisms. The two octahedra that remain unchanged here (green) may be thought of as pairings between two square pyramids. In positions that underwent a single gyration, we have pairings between square pyramids and triangular prisms, and in positions that underwent two gyrations, we have pairings between two triangular prisms.
The parts corresponding to the cantellated tesseract's triangular prisms are triangular prisms, where they haven't been affected by a gyration, and square pyramids, where they have. Six of these positions around the nearest J37 are triangular prisms, and the other 6 are square pyramids:
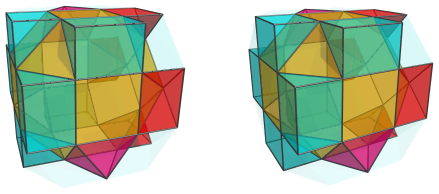
For clarity, we have omitted the previous pairs of cells corresponding with the cantellated tesseract's octahedra. Here are all the cells together:
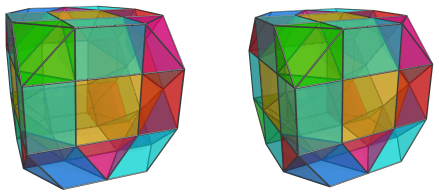
These are all the cells that lie on the near side of the biparabigyrated cantellated tesseract.
The Limb
On the limb of the biparabigyrated cantellated tesseract are six J37 cells:
These cells, like other cells on the limb, are seen at a 90° angle, and so they appear flattened into octagons. This is merely an artifact of the projection; in 4D they are full-bodied Johnson solids.
Four of these J37's are joined to each other along their axes of symmetry, forming a cycle:
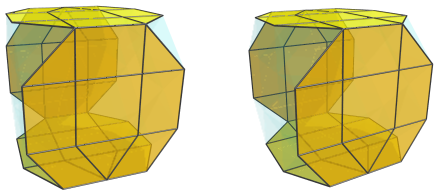
The other two J37's are joined to the J37 on the near side along its axis of symmetry and also to the 8th J37 on the far side, thus forming another cycle orthogonal to this cycle. The part of this cycle on the near side is shown below:
The next image shows the part of this cycle on the far side, with the far cell outlined in red:
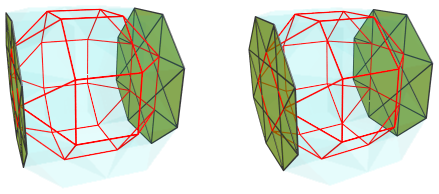
Notice that the orientation of the nearest J37 is opposite of that of the farthest J37. The nearest J37 and the farthest J37 connect to opposite ends of the two “flattened” J37's on the limb: remember that the flattening is merely an artifact of the projection, so the mismatching configurations of the square faces where these cells are connected are actually separated by the length of the limb J37's.
Back to the limb cells, the 8 remaining triangular gaps seen earlier are filled in by 4 square pyramids (red) and 4 triangular prisms (cyan):
Even though, due to foreshortening, both the triangular prisms and the square pyramids appear as triangles here, they should not be confused with each other. The 3 edges of each prism's triangular image are the projections of its square faces, whereas 2 of the 3 edges of each square pyramid's triangular image are the projections of its triangular faces, and the last edge is the projection of its square base. To help visualize this, the image below shows which edges are projections of triangular faces (red) and which edges are projections of square faces (black):
To make the orientation of the square pyramids easier to see, we also highlight their apices in red.
Here are all the limb cells together:
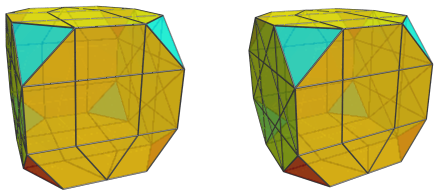
The Far Side
Past this point, we reach the cells on the far side of the biparabigyrated cantellated tesseract. We have already seen the outline of the J37 antipodal to the nearest J37 earlier; now we show it in full:
For clarity, we omit all the other cells we have seen so far.
On the right side of this J37 are two octahedral cells:
These octahedra are antipodal to the two octahedra on the near side that we saw at the beginning.
The other two triangular faces on the right side of the J37 are joined to two square pyramids:
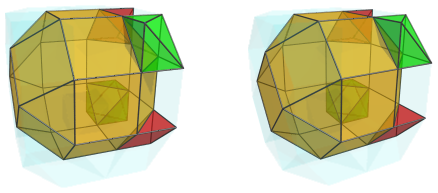
These square pyramids are antipodal to the square pyramids on the left side of the nearest J37. They are paired with two triangular prisms:
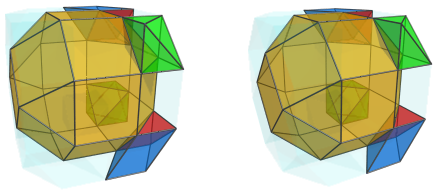
On the left side, there are two triangular prisms opposite the octahedra:
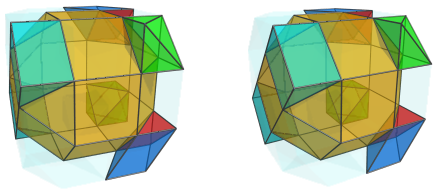
They are paired with two more square pyramids:
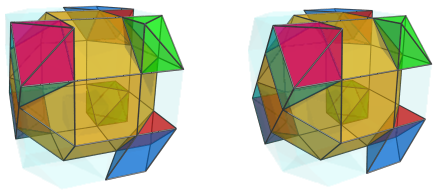
Opposite the square pyramids on the right side of the J37 are two more triangular prisms on the left:
They are paired with other triangular prisms:
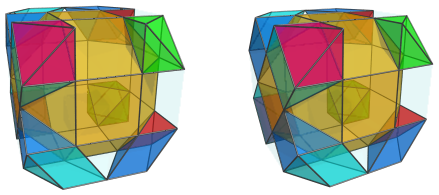
As should be obvious by now, this arrangement of cells is the exact mirror image of the cells on the near side. So it should be unsurprising that the 12 remaining gaps are also filled in by the mirror image of the arrangement of cells on the near side:
Finally, here are all the far side cells together:
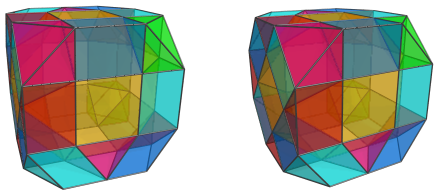
Summary
The following table summarizes the cells counts of the biparabigyrated cantellated tesseract:
| Region | Position |  |
 |
 |
 |
|---|---|---|---|---|---|
| Near side | Central | 1 | 0 | 0 | 0 |
| Corners | 0 | 2 | 4 | 8 | |
| Lateral | 0 | 0 | 6 | 6 | |
| Subtotal | 1 | 2 | 10 | 14 | |
| Equator | 6 | 0 | 4 | 4 | |
| Far side | Corners | 0 | 2 | 4 | 8 |
| Lateral | 0 | 0 | 6 | 6 | |
| Central | 1 | 0 | 0 | 0 | |
| Subtotal | 1 | 2 | 10 | 14 | |
| Grand total | 8 | 4 | 24 | 32 | |
Coordinates
The Cartesian coordinates of the biparabigyrated cantellated tesseract, centered on the origin and having edge length 2, are:
|
|
These are the coordinates of the cantellated tesseract with the vertices of 4 squares rotated by 45° in their respective planes.
