The Runcinated Snub 24-cell
The runcinated snub 24-cell, also variously known as the prismatorhombato snub 24-cell, or the runcinated snub demitesseract, or by the Bowers Acronym prissi, is a CRF polychoron derived from the snub 24-cell. Its surface consists of 288 vertices, 1008 edges, 960 polygons, and 240 cells (24 icosahedra, 24 truncated tetrahedra, 96 triangular cupolae (J3), and 96 triangular prisms).

It can be constructed by radially displacing the icosahedral cells of the snub 24-cell outwards until they are an edge length apart, and filling in the resulting gaps with truncated tetrahedra, triangular cupolae, and triangular prisms. It is vertex-transitive but not uniform, and thus belongs to the category of scaliform polytopes.
It was discovered by Richard Klitzing in 2005.
Structure
We shall explore the runcinated snub 24-cell by means of its parallel projections into 3D, centered on an icosahedral cell.
The Near Side

This image shows the nearest cell to the 4D viewpoint, an icosahedron. Of its 20 triangular faces, 8 are joined to triangular prisms, shown next:

The remaining 12 faces of the icosahedron are joined to 12 triangular cupolae:




These cupolae come in 6 pairs, with their hexagonal faces sharing an edge. These hexagonal faces are joined to 6 truncated tetrahedra:

These truncated tetrahedra touch 6 of the starting icosahedron's edges.
The remaining exposed square faces of the triangular cupolae are joined to 12 more triangular prisms:

These triangular prisms look distorted, but that's only because they are being seen from an oblique angle with respect to the 4D viewpoint. In 4D, they are perfectly uniform.
Between these triangular prisms and the hexagonal faces of the truncated tetrahedra are 12 more triangular cupolae:

It should be obvious by now that the depressions forming around the triangular faces of the triangular prisms we've seen so far are where another 8 icosahedra fit into:

The exposed square faces of the triangular cupolae are joined to 24 more triangular prisms:
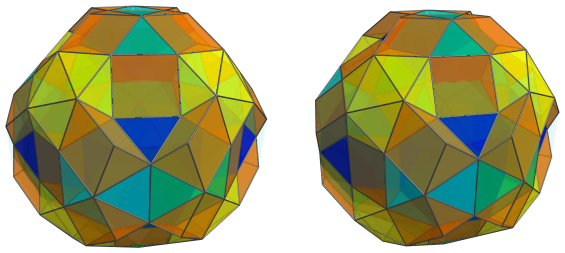
Nestled between these triangular prisms, the icosahedra, and the previous set of triangular prisms are another 12 triangular cupolae:
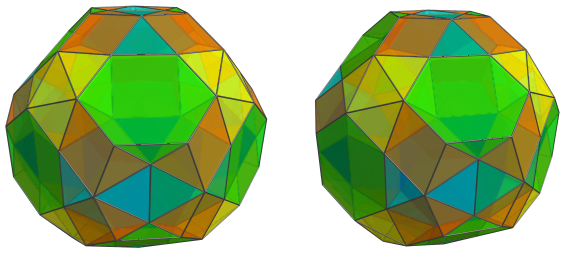
These are all the cells that lie on the near side of the polychoron. Next,
we come to the cells that lie on the limb of the projection (the equator
of the polytope).
The Equator
On the equator of the runcinated snub 24-cell are 6 icosahedra:

These icosahedra have been foreshortened into hexagons, because they lie perpendicular to the 4D viewpoint. In reality, they are perfectly regular icosahedra.
Between these icosahedra are 12 truncated tetrahedra:

These truncated tetrahedra lie at a 90° angle to the 4D viewpoint, and so they have been foreshortened into irregular pentagons. In 4D, however, they are perfectly uniform truncated tetrahedra. Their tips that touch the icosahedra are actually edges that have been foreshortened into points; thus they form bridges between some of the edges of the 6 icosahedra.
Between these truncated tetrahedra are 8 triangular prisms:

These triangular prisms lie at a 90° angle from the 4D viewpoint, and thus have been foreshortened into triangles. The edges that they share with the truncated tetrahedra have been foreshortened into points.
The final gaps in the above image are filled in by 24 triangular cupolae:

These cupolae appear as irregular trapeziums because they lie at a 90° angle with the 4D viewpoint, and are seen laterally.
These are all the cells that lie on the limb of the runcinated snub 24-cell. Past this point, the arrangement of cells on the far side mirror the arrangement on the near side.
Summary
The following table summarizes the cell counts of the runcinated snub 24-cell:
| Region | Layer | ||||
|---|---|---|---|---|---|
| Near side | 1 | 1 | 8 | 12 | 0 |
| 2 | 8 | 12 | 12 | 6 | |
| 3 | 0 | 24 | 12 | 0 | |
| Subtotal | 9 | 44 | 36 | 6 | |
| Equator | 6 | 8 | 24 | 12 | |
| Far side | 3 | 0 | 24 | 12 | 0 |
| 2 | 8 | 12 | 12 | 6 | |
| 1 | 1 | 8 | 12 | 0 | |
| Subtotal | 9 | 44 | 36 | 6 | |
| Grand total | 24 | 96 | 96 | 24 | |
| 240 cells | |||||
Coordinates
The Cartesian coordinates of the runcinated snub 24-cell, centered on the origin with edge length 2 are all even permutations of coordinate and all changes of sign of:
- (0, 1, φ, 3+φ)
- (1, 2, φ2, 2+φ)
where φ is the Golden Ratio, (1+√5)/2.




