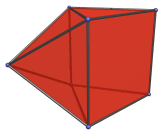
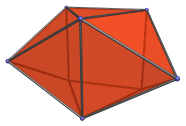
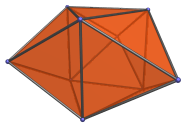
The Triangular Prism

---

The triangular prism is a simple 3D uniform polyhedron bounded by 5 polygons (2 triangles and 3 squares), 9 edges, and 6 vertices. It may be considered to be the extrusion of the triangle.

Two triangular prisms can be glued together at their square faces in gyro orientation to produce a gyrobifastigium (J26), a Johnson solid:

Besides the obvious construction as the extrusion of the triangle, the triangular prism may also be considered as a digonal cupola: just as the triangular cupola can be constructed as the convex hull of a triangle and a Stott-expanded triangle (hexagon) on parallel planes, so the triangular prism can be constructed as the convex hull of a digon and a Stott-expanded digon (square) on parallel planes. Thus, the gyrobifastigium may be considered to be a digonal gyrobicupola, which explains its place as the 26th Johnson solid, the first among the bicupolae.

The triangular prism can also be augmented by up to 3 square pyramids, forming the augmented triangular prism (J49), the biaugmented triangular prism (J50), and the triaugmented triangular prism (J51).

The dual of the triangular prism is the triangular bipyramid (with isosceles triangular faces). Note that this is not to be confused with the Johnson solid triangular bipyramid (J12), whose faces are equilateral triangles. J12 is the dual of a non-uniform triangular prism that has rectangular rather than square faces (edge ratio √6 : 1).

Projections

In order to be able to identify the triangular prism in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:

Projection	Envelope	Description
	Triangle	Parallel projection centered on a triangular face.
	Square	Parallel projection centered on a vertical edge.
	Rectangle	Parallel projection parallel to a square face. The left edge of the projection is the image of a square face.
	Non-uniform pentagon	Vertex-centered parallel projection.

Coordinates

The Cartesian coordinates of the triangular prism, centered on the origin and having edge length 2, are:

• (±1, −1/√3, ±1)
• (0, 2/√3, ±1)

Occurrences

The triangular prism is a very versatile polyhedron that occurs in many 4D uniform polytopes, including:

• The cantellated 5-cell;
• The runcinated 5-cell;
• The cantitruncated 5-cell;
• The runcitruncated 5-cell;
• The cantellated tesseract;
• The runcinated tesseract;
• The cantitruncated tesseract;
• The runcitruncated tesseract;
• The cantellated 24-cell;
• The runcinated 24-cell;
• The cantitruncated 24-cell;
• The runcitruncated 24-cell;
• The cantellated 120-cell;
• The runcinated 120-cell;
• The cantitruncated 120-cell;
• The runcitruncated 120-cell;
• The 3,n-duoprisms, such as the 3,3-duoprism and the 3,4-duoprism.

It also occurs in many CRF polychora, including (but not limited to):

• Cube atop icosahedron (K4.21);
• The tetrahedral canticupola (K4.76);
• The square magnabicupolic ring (K4.105);
• Octahedron atop rhombicuboctahedron (K4.107);
• Cuboctahedron atop Truncated Cube (K4.129);
• The tetrahedral magnaursachoron;
• The augmented cantitruncated 5-cell;
• The octa-augmented runcinated tesseract;
• The octa-augmented truncated tesseract;
• The octa-augmented runcitruncated 16-cell;
• The biparabigyrated cantellated tesseract;
• The runcinated snub 24-cell;
• The bilunabirotunda pseudopyramid;
• The triangular hebesphenorotundaeic rhombochoron.