The Runcitruncated Tesseract
The runcitruncated tesseract is a uniform polytope in the tesseract family. It is bounded by 80 cells (8 truncated cubes, 16 cuboctahedra, 24 octagonal prisms, 32 triangular prisms), 368 polygons (128 triangles, 192 squares, 48 octagons), 480 edges, and 192 vertices.
It can be constructed by expanding the truncated cubes of the truncated tesseract outwards radially. The tetrahedra get expanded into cuboctahedra, and the remaining gaps can be filled in by triangular prisms and octagonal prisms.
Structure
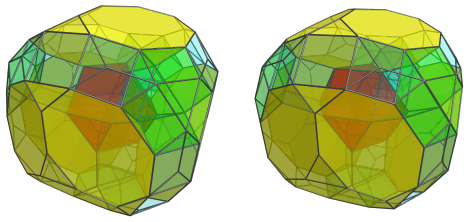
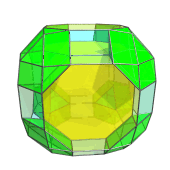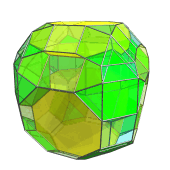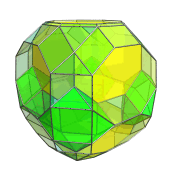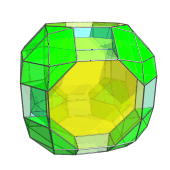
The structure of the runcitruncated tesseract can be easily discerned from its parallel projection into 3D.
The above image shows the projection centered on a truncated cube. The truncated cube in the center of the image is the closest cell to the 4D viewpoint. For clarity, we have rendered all the other cells in a light transparent color.
Six octagonal prisms surround this nearest cell:
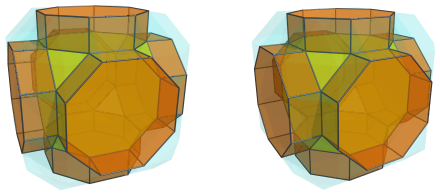
Eight cuboctahedra touch the remaining 8 triangular faces of the nearest cell:
Straddling the octagonal prisms and cuboctahedra are 12 triangular prisms:
These are all the cells that lie on the near side of the runcitruncated tesseract. Surrounding them are the cells on the “equator”, among which are 6 more truncated cubes:
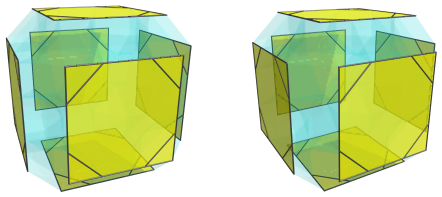
These truncated cubes appear to be flattened into squares, because they are being seen from a 90° angle. In 4D, they are perfectly uniform truncated cubes. For clarity, we have omitted the cells on the near side that we have seen previously.
There are also 12 octagonal prisms on the equator that straddle the truncated cubes:
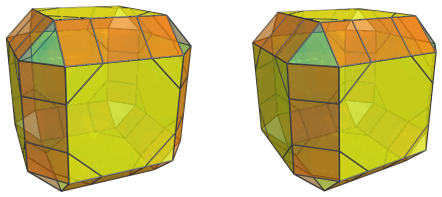
These octagonal prisms have been foreshortened into rectangles, because they are also being seen from a 90° angle; in 4D, they are perfectly uniform octagonal prisms.
Finally, the remaining triangular gaps are filled by 8 triangular prisms, which appear foreshortened into triangles—they are being seen from a 90° angle as well:
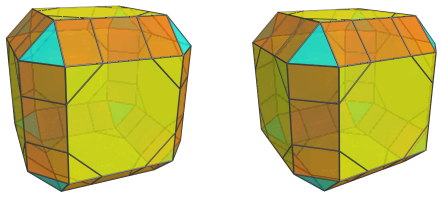
These are all the cells that lie on the equator. Past this point, we reach the cells on the far side of the runcitruncated tesseract, whose arrangement exactly mirrors the arrangement of cells on the near side.
The following table summarizes the cell counts in the near side, equator, and far side:
| Region |  |
 |
 |
 |
|---|---|---|---|---|
| Near side | 1 | 12 | 6 | 8 |
| Equator | 6 | 8 | 12 | 0 |
| Far side | 1 | 12 | 6 | 8 |
| Total | 8 | 32 | 24 | 16 |
| Grand total | 80 cells | |||
Animations
This is a stereographic animation of the runcitruncated tesseract rotating in the WY and XZ planes, projected into 3D:
To reduce clutter, only truncated cubes and cuboctahedra are shown, and cells on the far side of the polytope are culled. As a result, some cells may appear to pop out of nowhere; in reality, they are actually just coming into view as the polychoron rotates. The “shadowy” cuboctahedra are the outlines of cuboctahedra that are hovering just on the limb of the polychoron, about to come into view. They become solid as they emerge on the near side.
Coordinates
The coordinates of the runcitruncated tesseract are all permutations of coordinates and changes of sign of:
- (1, 1+√2, 1+√2, 1+2√2)
