The Bitruncated 5-cell

---

The bitruncated 5-cell is a cell-transitive polychoron bounded by 10 truncated tetrahedra, 40 polygons (20 triangles and 20 hexagons), 60 edges, and 30 vertices. It is formed by truncating a pentachoron at halfway to the depth that would yield a dual pentachoron. Its 10 cells are in two groups of 5, each group corresponding respectively to the cells of a pentachoron and those of its dual. Due to the equivalence between these two groups of cells, it has a higher degree of symmetry than the 5-cell itelf.

The dual of the bitruncated 5-cell is the bidecachoron, a Catalan polychoron.

Projections

The following image shows the cell-first perspective projection of the bitruncated 5-cell into 3D:

For clarity, we have omitted cells that lie on the far side of the polytope. The nearest cell to the 4D viewpoint is a truncated tetrahedron, shown below:

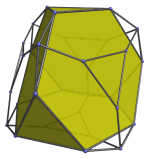
Surrounding this cell are 4 other truncated tetrahedra, as shown below:

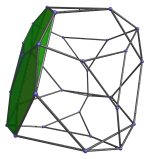
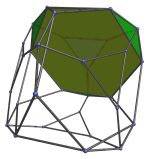
These cells look flattened because of foreshortening by the perspective projection. They are actually all uniform truncated tetrahedra. They are joined to each other by triangular faces.

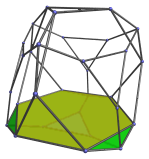
The other triangular faces of these 4 cells are connected to the antipodal truncated tetrahedron lying on the opposite side of the polychoron:

As can be seen, the antipodal truncated tetrahedron lies in a dual orientation to the nearest truncated tetrahedron.

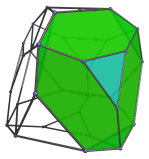
The triangular faces of the nearest cell, on the other hand, are connected to the four cells surrounding the far-side cell, shown below:

For reference, we have included the farthest cells in these images.

Comparing these images with the earlier ones, we see that these cells are joined to the four cells surrounding the nearest cell by their hexagonal faces.

Altogether, these are the 10 cells that bound the bitruncated 5-cell.

Properties

The bitruncated 5-cell is one of the cell-transitive uniform polychora that aren't regular. Besides the n,n-duoprisms, the other such polychoron is the bitruncated 24-cell.

Coordinates

The Cartesian coordinates of the bitruncated 5-cell, centered on the origin and having edge length 2, are:

• ±(0, 4/√6, 4/√3, 0)
• ±(0, 4/√6, −2/√3, ±2)
• ±(5/√10, 1/√6, 4/√3, 0)
• ±(5/√10, 1/√6, −2/√3, ±2)
• ±(5/√10, 5/√6, 2/√3, 0)
• ±(5/√10, 5/√6, −1/√3, ±1)
• ±(5/√10, −3/√6, 0, ±2)
• ±(5/√10, −3/√6, ±3/√3, ±1)

Simpler coordinates can be obtained in 5D as all permutations of coordinates of:

• (0, 0, √2, 2√2, 2√2)

The 4D coordinates are derived by projecting these 5D coordinates back into 4D using a symmetric projection.