The Cantitruncated 24-cell

---

The cantitruncated 24-cell is a uniform polychoron in the 24-cell family. Its surface consists of 144 cells (24 great rhombicuboctahedra, 24 truncated cubes, 96 triangular prisms), 720 polygons (192 triangles, 288 squares, 96 hexagons, 144 octagons), 1152 edges, and 576 vertices.

It may be constructed from the bitruncated 24-cell by radially expanding 24 truncated cubes outwards, causing the other 24 truncated cubes to expand into great rhombicuboctahedra, and filling in the remaining gaps with triangular prisms.

Structure

We shall explore the structure of the cantitruncated 24-cell using its parallel projections into 3D, centered on a great rhombicuboctahedron.

The above image shows one of the 24 great rhombicuboctahedral cells. It is the nearest cell to the 4D viewpoint.

Its square faces are joined to 12 triangular prisms, shown next:

The octagonal faces of the nearest cell are joined to 6 truncated cubes:

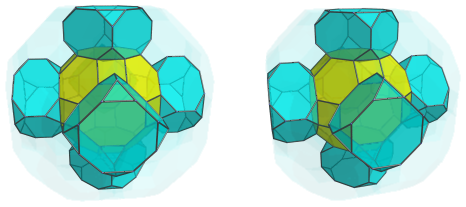
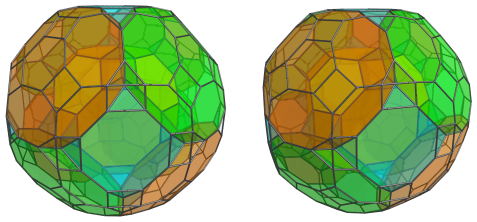
The hexagonal faces of the nearest cell are joined to 8 other great rhombicuboctahedra:

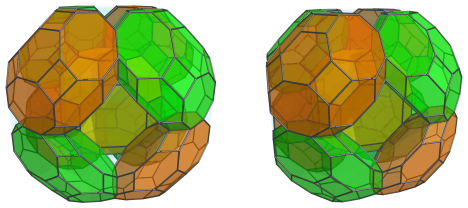
Here's all these cells together:

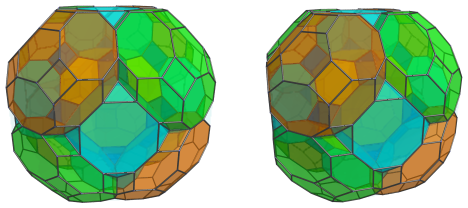
There are 24 remaining gaps here, between each truncated cube and a pair of great rhombicuboctahedra. They are where another 24 triangular prisms are fitted:

These are all the cells that lie on the near side of the cantitruncated 24-cell. Past this point, we reach its limb, or “equator”, where there are 6 great rhombicuboctahedra:

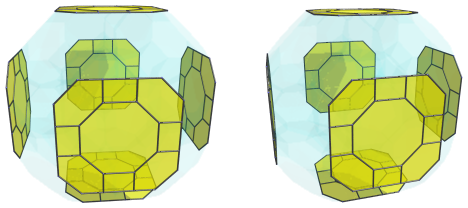
For clarity, we have omitted the cells we have seen previously. These great rhombicuboctahedra appear to be flattened into octagons; this is because they are being seen from a 90° angle. In 4D, they are perfectly uniform great rhombicuboctahedra.

There are another 12 truncated cubes on the equator, shown next:

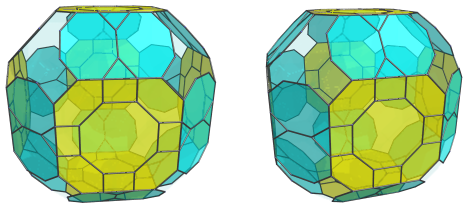
As with the previous cells, these truncated cubes also appear to be flattened into octagons; however, in 4D they are perfectly uniform truncated cubes. This flattening effect is merely a foreshortening caused by the projection into 3D.

Another 24 triangular prisms fit into the gaps straddling the truncated cubes and the great rhombicuboctahedra:

These triangular prisms have also been foreshortened into rectangles due to their being seen from a 90° angle. In 4D, they are perfectly uniform triangular prisms. The edges of the rectangle that touch the cyan truncated cubes are the images of the triangular prism's triangular faces, and the edge touching the yellow great rhombicuboctahedron is the image of one of the triangular prism's square faces.

These are all the cells that lie on the limb of the cantitruncated 24-cell. The remaining hexagonal gaps are not the images of any cells; they are where 8 great rhombicuboctahedra on the near side of the polychoron touch their counterparts on the far side.

Past this point, we reach the far side of the polytope, where the arrangement of cells perfectly mirrors that of the near side. The following table summarizes the cell counts on the far and near sides and the equator:

Region
Near side	1+8=9	6	12+24=36
Equator	6	12	24
Far side	9	6	36
Grand total	24	24	96

Coordinates

The Cartesian coordinates of the cantitruncated 24-cell, centered on the origin with edge length 2, are all permutations of coordinates and changes of sign of:

• (1, 1+√2, 1+2√2, 3+3√2)
• (0, 2+√2, 2+2√2, 2+3√2)