The Great Rhombicuboctahedron
The great rhombicuboctahedron is a 3D uniform polyhedron bounded by 26 polygons (8 hexagons, 12 squares, and 6 octagons), 72 edges, and 48 vertices. It may be constructed by radially expanding the octagonal faces of the truncated cube outwards, or equivalently, radially expanding the hexagonal faces of the truncated octahedron, or the non-axial square faces of the rhombicuboctahedron.

The great rhombicuboctahedron is also known as the truncated cuboctahedron; however, this is a misnomer. Truncating the cuboctahedron does not yield a uniform polyhedron, only a non-uniform topological equivalent of the great rhombicuboctahedron. The correct derivation is as described above.
The dual of the great rhombicuboctahedron is the disdyakis dodecahedron, a Catalan solid.
Projections
In order to be able to identify the great rhombicuboctahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:
| Projection | Envelope | Description |
|---|---|---|
 |
Octagon | Parallel projection centered on an octagonal face. |
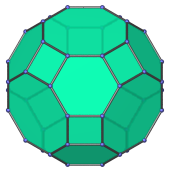 |
Dodecagon | Parallel projection centered on a hexagonal face. |
 |
Octagon | Parallel projection centered on a square face. |
Coordinates
The Cartesian coordinates of the great rhombicuboctahedron, centered on the origin and having edge length 2, are all permutations of coordinates and changes of sign of:
- (1, (1+√2), (1+2√2))
Occurrences
The great rhombicuboctahedron appears as cells in the following 4D uniform polytopes:
- The cantitruncated tesseract;
- The omnitruncated tesseract, its direct 4D analogue;
- The cantitruncated 24-cell;
- The omnitruncated 24-cell.




