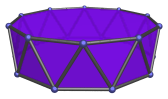
The Decagonal Antiprism

---

The decagonal antiprism is a 3D uniform polyhedron bounded by 22 polygons (2 decagons and 20 triangles), 40 edges, and 20 vertices.

The height of a decagonal antiprism with an edge length of 2 is:

2√(√(11φ+7)−2φ−1)

or approximately 1.724794, where φ=(1+√5)/2 is the Golden Ratio.

A decagonal antiprism can be attached to a pentagonal cupola (J5) to make a gyroelongated pentagonal cupola (J24), or attached to a pentagonal rotunda (J6) to make a gyroelongated pentagonal rotunda (J25).

Inserting a decagonal antiprism between two pentagonal cupolae produces the gyroelongated pentagonal bicupola (J46). Doing so between a pentagonal cupola and a pentagonal rotunda produces the gyroelongated pentagonal cupolarotunda (J47); and doing so between two pentagonal rotundae produces the gyroelongated pentagonal birotunda (J48).

Projections

Here are some views of the decagonal antiprism from various angles:

Projection	Envelope	Description
	Regular dodecagon	Parallel projection centered on decagonal face.
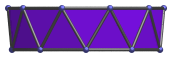	Trapezium	Parallel projection parallel to square faces and a pair of triangles.
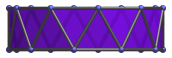	Rectangle	9° side view.
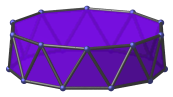	Hendecagon	Parallel projection centered on vertex.

Coordinates

The Cartesian coordinates of the decagonal antiprism, centered on the origin and having edge length 2, are:

• (±2φ, 0, H)
• (±1, ±√(3+4φ), H)
• (±φ², ±√(2+φ), H)
• (0, ±2φ, −H)
• (±√(3+4φ), ±1, −H)
• (±√(2+φ), ±φ², −H)

where φ = (1+√5)/2 is the Golden Ratio, and H = √(√(11φ+7)−2φ−1), or approximately 0.862397, is half the height of the antiprism.