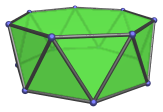
The Heptagonal Antiprism
The heptagonal antiprism is a 3D uniform polyhedron bounded by 16 polygons (2 heptagons and 14 triangles), 28 edges, and 14 vertices.
Projections
The following are some commonly-encountered views of the heptagonal antiprism:
| Projection | Description |
|---|---|
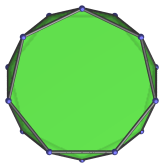 |
Heptagon-centered parallel projection. |
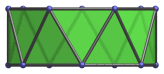 |
Parallel to a pair of opposite lateral edges. |
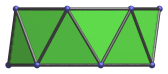 |
Parallel to a pair of opposite triangles. |
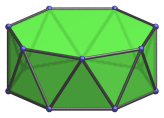 |
Vertex-centered parallel projection. |
Coordinates
The Cartesian coordinates of the heptagonal antiprism, centered on the origin and having edge length 2, are:
- (0, r, H)
- (±A, B, H)
- (±C, −D, H)
- (±1, −h, H)
- (0, −r, −H)
- (±A, −B, −H)
- (±C, D, −H)
- (±1, h, −H)
where r, A, B, C, D, h, and H are roots of the following polynomials within the indicated ranges:
| 7r6 − 56r4 + 112r2 − 64 = 0, | 2≤r≤3 |
| A3 − A2 − 2A + 1 = 0, | 1≤A≤2 |
| 7B6 − 21B4 + 14B2 − 1 = 0, | 1≤B≤2 |
| C3 − 2C2 − C + 1 = 0, | 2≤C≤3 |
| 7D6 − 14D4 + 7D2 − 1 = 0, | 0≤D≤1 |
| 7h6 − 35h4 + 21h2 − 1 = 0, | 2≤h≤3 |
| 7H6 − 7H4 + 1 = 0, | 0.8≤H≤0.9 |
r and h are the out-radius and in-radius, respectively, of a regular heptagon of edge length 2. H is half the height of the antiprism.
Their approximate values are:
- r = 2.304764870962486
- A = 1.801937735804838
- B = 1.436997392727370
- C = 2.246979603717467
- D = 0.512858431636277
- h = 2.076521396572336
- H = 0.858473196494555




