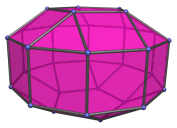
The Decagonal Prism

---

The decagonal prism is a 3D uniform polyhedron bounded by 12 polygons (2 decagonal faces and 10 squares), 30 edges, and 20 vertices. It may be considered to be the extrusion of the decagon.

A decagonal prism can be attached to a pentagonal cupola (J5) to form an elongated pentagonal cupola (J20), or to a pentagonal rotunda (J6) to form an elongated pentagonal rotunda (J21).

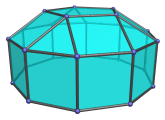
Attaching two cupolae to a decagonal prism produces the elongated pentagonal orthobicupola (J38) or the elongated pentagonal gyrobicupola (J39), depending on the orientation of the two cupolae relative to each other.

Replacing one of the cupolae with a pentagonal rotunda instead produces the elongated pentagonal orthocupolarotunda (J40) or the elongated pentagonal gyrocupolarotunda (J41), respectively.

Attaching two pentagonal rotunda to a decagonal prism produces the elongated pentagonal orthobirotunda (J42) or the elongated pentagonal gyrobirotunda (J43), depending on the orientation of the rotundae with respect to each other.

Projections

In order to be able to identify the decagonal prism in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:

Projection	Envelope	Description
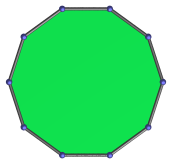	Regular decagon	Decagon-centered parallel projection.
	Rectangle	Parallel projection centered on a vertical edge.
	Rectangle	Square-centered parallel projection.
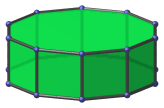	Decagon	Vertex-centered parallel projection.

Coordinates

The Cartesian coordinates of the decagonal prism, centered on the origin and having edge length 2, are all changes of sign of:

• (2φ, 0, 1)
• (1, √(3+4φ), 1)
• (φ², √(2+φ), 1)

where φ=(1+√5)/2 is the Golden Ratio.

Occurrences

The decagonal prism occurs in the following uniform polychora:

• The runcitruncated 120-cell;
• The omnitruncated 120-cell;
• The 5,10-duoprism.

It also occurs in the following CRF polychora:

• The deca-augmented 5,10-duoprism.