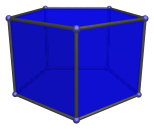
The Pentagonal Prism
The pentagonal prism is a 3D uniform polyhedron bounded by 7 polygons (2 pentagons and 5 squares), 15 edges, and 10 vertices. It may be considered to be the extrusion of the pentagon.
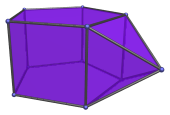
The pentagonal prism can be augmented by a square pyramid to form the augmented pentagonal prism (J52), a Johnson solid. A second square pyramid can be added at a non-adjacent position to produce the biaugmented pentagonal prism (J53).
The dual of the pentagonal prism is the pentagonal bipyramid. Not to be confused with its topological Johnson solid analogue J13, but a non-Johnson pentagonal bipyramid among the uniform duals which include the Catalan solids.
Projections
In order to be able to identify the pentagonal prism in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:
| Projection | Envelope | Description |
|---|---|---|
 |
Regular pentagon | Parallel projection centered on a pentagonal face. |
 |
Rectangle | Parallel projection centered on a vertical edge. |
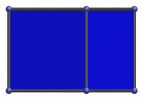 |
Rectangle | Parallel projection parallel to a square face. The left edge of the projection envelope is the image of a square face. |
Coordinates
The Cartesian coordinates of the pentagonal prism, centered on the origin and having edge length 2, are:
- (√((10+2√5)/5), 0, ±1)
- (√((5−√5)/10), ±φ, ±1)
- (−√((5+2√5)/5), ±1, ±1)
where φ=(1+√5)/2 is the Golden Ratio.
Occurrences
The pentagonal prism occurs in the following 4D uniform polytopes:
- The runcinated 120-cell;
- The cantellated 600-cell;
- The cantitruncated 600-cell;
- The runcitruncated 600-cell;
- The 5,10-duoprism;
- The 5,20-duoprism.
The pentagonal prism also occurs in the following CRF polychora: