The Hexagonal Prism
The hexagonal prism is a 3D uniform polyhedron bounded by 8 polygons (2 hexagons and 6 squares), 18 edges, and 12 vertices. It is the extrusion of the hexagon into 3D.
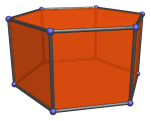
Attaching a triangular cupola to a hexagonal prism produces the elongated triangular cupola (J18), a Johnson solid. Attaching a second triangular cupola produces either the elongated triangular orthobicupola (J35) or the elongated triangular gyrobicupola (J36), depending on whether the second cupola is aligned or rotated with respect to the first, respectively.
The hexagonal prism can be augmented by up to 3 square pyramids to produce a series of convex augmented prisms, which are Johnson solids:
- The augmented hexagonal prism (J54);
- The parabiaugmented hexagonal prism (J55);
- The metabiaugmented hexagonal prism (J56);
- The triaugmented hexagonal prism (J57).
Projections
In order to be able to identify the hexagonal prism in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:
| Projection | Envelope | Description |
|---|---|---|
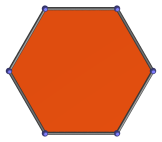 |
Regular hexagon | Hexagon-centered parallel projection. |
 |
Rectangle | Parallel projection centered on a vertical edge. |
 |
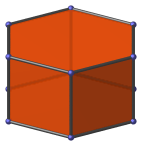
Rectangle | Square-centered parallel projection. |
 |
Hexagon | Vertex-centered parallel projection. |
Coordinates
The Cartesian coordinates of the hexagonal prism, centered on the origin and having edge length 2, are:
- (±√3, ±1, ±1)
- (0, ±2, ±1)
Occurrences
The hexagonal prism occurs as cells in the following 4D uniform polytopes:
- The runcitruncated 5-cell;
- The omnitruncated 5-cell;
- The runcitruncated tesseract;
- The runcitruncated 16-cell;
- The omnitruncated tesseract;
- The runcitruncated 24-cell;
- The omnitruncated 24-cell;
- The runcitruncated 600-cell;
- The omnitruncated 120-cell.
It also occurs in a number of CRF polychora, including (but not limited to):




