The Runcitruncated 24-cell

---

The runcitruncated 24-cell is a beautiful uniform polychoron in the 24-cell family. It consists of 240 cells (24 truncated octahedra, 96 hexagonal prisms, 96 triangular prisms, 24 rhombicuboctahedra), 1104 polygons (192 triangles, 720 squares, 192 hexagons), 1440 edges, and 576 vertices. It may be constructed from the truncated 24-cell by radially expanding the 24 truncated octahedra outwards.

Perspective Projections

Centered on truncated octahedron

The following image shows a perspective projection of the runcitruncated 24-cell into 3D, centered on a truncated octahedron:

The nearest truncated octahedron (red) to the 4D viewpoint lies in the center of this projection. Eight other truncated octahedra (yellow) lie adjacent to it, in cubic formation. The green cells are rhombicuboctahedra. For clarity, cells that lie on the far side are omitted, along with the triangular prisms and hexagonal prisms.

Centered on rhombicuboctahedron

The next image shows another projection of the runcitruncated 24-cell, this time centered on a rhombicuboctahedron:

The nearest cell to the 4D viewpoint here is the blue rhombicuboctahedron at the center of the projection image. It is surrounded by 6 truncated octahedra (yellow). Another 8 rhombicuboctahedra (green) straddle these truncated octahedra. Again, for clarity's sake, the triangular and hexagonal prisms are omitted, as are the cells that lie on the far side of the runcitruncated 24-cell.

Notice that this layout of cells corresponds with the layout in the previous projection, with the roles of the rhombicuboctahedra and the truncated octahedra swapped. This is a consequence of the fact that the rhombicuboctahedral cells correspond with the cells of a 24-cell, and the truncated octahedra correspond with the cells of a dual 24-cell. Since the 24-cell is self-dual, these two types of cells are laid out in the same way, and exhibit equivalent relationships with each other.

Parallel Projections

The following image shows a projection of the runcitruncated 24-cell, centered on a truncated octahedron. This time, we use a parallel projection for exploring the structure of the polytope.

The truncated octahedron in the center is the closest cell to the 4D viewpoint. For clarity, we render all other cells in a light transparent color.

As we have seen in the perspective projections, six rhombicuboctahedra surround this nearest cell, as shown next:

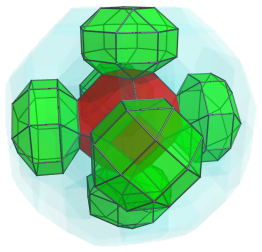
These rhombicuboctahedra look a bit flattened, because they are seen at a 45° angle. In 4D, they are perfectly uniform. They each share a square face with the nearest cell.

The hexagonal faces of the nearest cell are shared with 8 hexagonal prisms, shown next:

Touching the edges of the nearest cell are 12 triangular prisms:

Here are the preceding cells, all together:

The exposed hexagonal faces of the 8 hexagonal prisms are joined to another 8 truncated octahedra, shown next:

The gaps between these cells are obviously filled by hexagonal prisms:

The exposed triangular faces of the rhombicuboctahedra are joined to another 24 triangular prisms:

Straddled between these triangular prisms are also another 24 hexagonal prisms:

All the cells seen so far lie on the near side of the runcitruncated 24-cell. The next layer of cells lie on the “equator”: they are oriented 90° from the 4D viewpoint. Among these equatorial cells are 6 truncated octahedra, shown below:

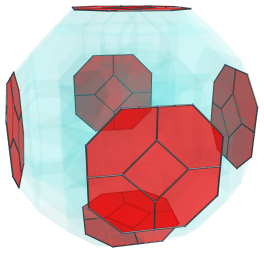
For clarity, we omit the other cells that we have seen before. These truncated octahedra have been foreshortened into octagons, because they are seen at a 90° angle. In 4D, they are perfectly uniform truncated octahedra.

These truncated octahedra are bridged by 12 rhombicuboctahedra, shown next:

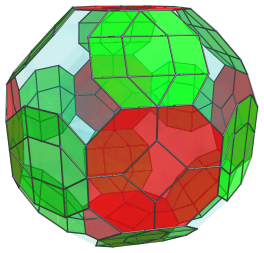
Again, these rhombicuboctahedra are perfectly uniform in 4D, but they have been foreshortened into octagons because they are at a 90° angle with the line-of-sight.

These rhombicuboctahedra themselves are bridged by 8 hexagonal prisms, as seen below:

These hexagonal prisms have been foreshortened into hexagons.

The remaining square gaps in the runcitruncated 24-cell's equator are filled in by triangular prisms, 24 of them:

These triangular prisms, of course, have also been foreshortened; they appear as rectangles. They each share an edge with a red truncated octahedron. The apparent edges they share with the green rhombicuboctahedra are actually the foreshortened images of their triangular faces. The apparent edges they share with the hexagonal prisms are actually the foreshortened images of one of their square faces.

Past this point are the cells on the far side of the runcitruncated 24-cell. They follow an identical layout with the cells on the near side that we have already seen, except in reverse order of layers.

Therefore, in summary, on the near side we have 1+8=9 truncated octahedra, 6 rhombicuboctahedra, 8+12+24=44 hexagonal prisms, and 12+24=36 triangular prisms. On the equator we have 6 truncated octahedra, 12 rhombicuboctahedra, 8 hexagonal prisms, and 24 triangular prisms. On the far side, we have again 9 truncated octahedra, 6 rhombicuboctahedra, 44 hexagonal prisms, and 36 triangular prisms. Thus, in total, there are 9+6+9=24 truncated octahedra, 6+12+6=24 rhombicuboctahedra, 44+8+44=96 hexagonal prisms, and 36+24+36=96 triangular prisms, corresponding with the cells, ridges, edges, and vertices of a 24-cell, from which the runcitruncated 24-cell is derived.

Coordinates

The coordinates for the runcitruncated 24-cell are all permutations of coordinates and changes of sign of:

• (0, √2, 2√2, 2+3√2)
• (1, 1+√2, 1+2√2, 1+3√2)

These coordinates yield an origin-centered runcitruncated 24-cell with edge length 2.

The second set of coordinates coincides with the coordinates of an inscribed omnitruncated tesseract.