The Bitruncated Tesseract

---

The bitruncated tesseract is a uniform polychoron constructed by truncating a tesseract halfway to the depth that would yield the dual 16-cell. Equivalently, it can be derived from the 16-cell by truncating at halfway the depth that would yield the dual tesseract. Hence, it is also known as the bitruncated 16-cell. It is bounded by 24 cells (8 truncated octahedra, 16 truncated tetrahedra), 120 polygons (32 triangles, 24 squares, 64 hexagons), 192 edges, and 96 vertices.

The following image shows the perspective projection of the bitruncated tesseract, centered on one of the truncated octahedral cells:

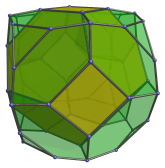
Structure

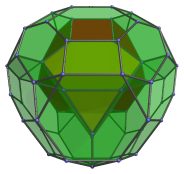
We shall explore the structure of the bitruncated tesseract by examining its parallel projection into 3D:

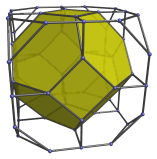
This image shows its parallel projection centered on a truncated octahedron. The truncated octahedron shown here is the one closest to the 4D viewpoint. Its hexagonal faces are joined to 8 truncated tetrahedra, shown in the next two images:

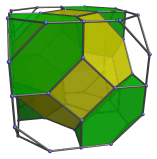
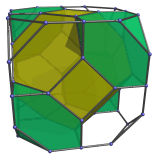
These truncated tetrahedra are joined to each other via their triangular faces, and to the truncated octahedra via their hexagonal faces.

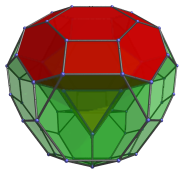
The square faces of the central truncated octahedron are joined to 6 other truncated octahedra, shown in the following images:

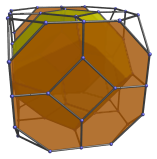
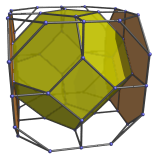
These 6 truncated octahedra lie at a 90° angle to the 4D viewpoint, so they appear to be flat octagons due to foreshortening. In reality, they are perfectly uniform truncated octahedra.

The central truncated octahedron and the 8 truncated tetrahedra may be thought of as lying on the “northern hemisphere” of the bitruncated tesseract. The 6 equatorial cells lie on the “equator”. On the other side of the bitruncated tesseract, the “southern hemisphere”, are another 9 cells that mirror the layout of the northern hemiphere cells. Thus, this makes a total of 1+6+1=8 truncated octahedra, and 8+8=16 truncated tetrahedra.

Other Projections

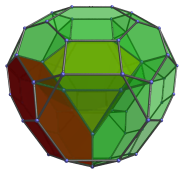
The following image shows the perspective projection of the bitruncated tesseract, centered on a truncated tetrahedron:

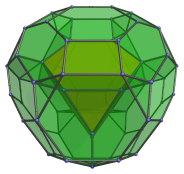
The nearest truncated tetrahedron is shown here in yellow. The 4 truncated tetrahedra surrounding it are shown below:

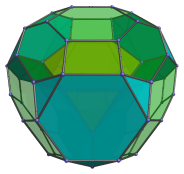
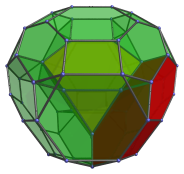
There are also 4 truncated octahedra surrounding the nearest cell, shown in the following images:

Coordinates

The coordinates of the vertices of the bitruncated tesseract are all permutations of coordinates and changes of sign of:

• (0, √2, 2√2, 2√2)