The Rectified 120-cell

---

The rectified 120-cell is a uniform polychoron bounded by 120 icosidodecahedra and 600 tetrahedra, for a total of 720 cells, 3120 polygons (2400 triangles, 720 pentagons), 3600 edges, and 1200 vertices.

The 600 tetrahedra correspond with the 600 tetrahedra in the 600-cell, although here they are in dual orientation. The gaps between these 600 tetrahedra are filled in by 120 icosidodecahedra, corresponding with the 120 dodecahedra of the 120-cell.

Structure

We shall explore the structure of the rectified 120-cell by means of its parallel projection into 3D, centered on an icosidodecahedron.

The 600 Tetrahedra

First, we look at the layout of the 600 tetrahedra. They may be grouped into 14 layers, each of which corresponds with the symmetry of a 3D icosahedral polyhedron. Half of the layers corresponds with the “northern hemisphere” of the rectified 120-cell, and the other half corresponds with the “southern hemisphere”. The two equatorial layers have some overlap. The first layer corresponds with the 20 faces of the icosahedron:

For clarity, we have omitted all edges except those on the 20 tetrahedra and those on the limb of the projection.

The next layer also corresponds with the faces of an icosahedron, albeit slightly larger. They each share a vertex with one of the 20 tetrahedra from the first layer.

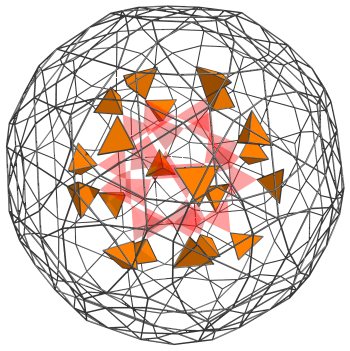
For reference, we include the 20 tetrahedra from the first layer, rendered in transparent red.

The third layer consists of 30 tetrahedra that straddle the tetrahedra in the second layer. They correspond with the vertices of an icosidodecahedron:

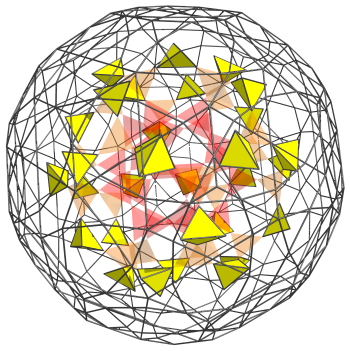
Again, for reference, we leave in the previous two layers' tetrahedra in transparent color.

The next layer consists of 60 tetrahedra, corresponding with the vertices of a truncated icosahedron (a “buckyball”):

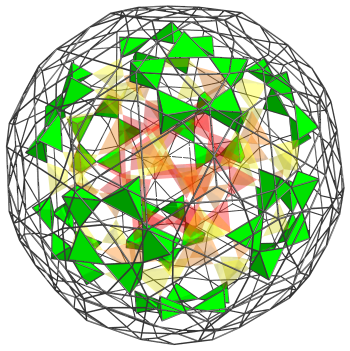
The fifth layer consists of another 60 tetrahedra, corresponding with the vertices of another truncated icosahedron:

The sixth layer consists of yet another 60 tetrahedra, corresponding with the vertices of a rhombicosidodecahedron:

The last layer, the seventh layer, consists of 80 tetrahedra, corresponding with the vertices of a truncated rhombic triacontahedron. They are of two distinct categories: 20 tetrahedra, corresponding to the vertices of a dodecahedron, and 60 tetrahedra, corresponding to the vertices of another rhombicosidodecahedron. The 60 tetrahedra come in 12 circles of 5 tetrahedra each.

The 20 tetrahedra lie strictly in the “northern hemisphere” of the rectified 120-cell; whereas the other 60 tetrahedra actually lie on the “equator”, and are thus shared with the corresponding seventh layer of the “southern hemisphere”. The following image shows all of the northern hemisphere (and equatorial) tetrahedra together:

From this point on, the layers repeat in reverse in the “southern hemisphere”. The seventh layer of the southern hemisphere shares the 60 equatorial tetrahedra, so it only adds another 20 tetrahedra to the total. So in total, we have 20+20+30+60+60+60+80=330 tetrahedra in the northern hemisphere (including the 60 at the equator), and 20+60+60+60+30+20+20=270 tetrahedra in the southern hemisphere. Thus, there are 600 tetrahedra in total.

The 120 Icosidodecahedra

So far, we have accounted for the 600 tetrahedral cells. Now we take a look at the 120 icosidodecahedral cells, starting with the icosidodecahedron nearest to the 4D viewpoint:

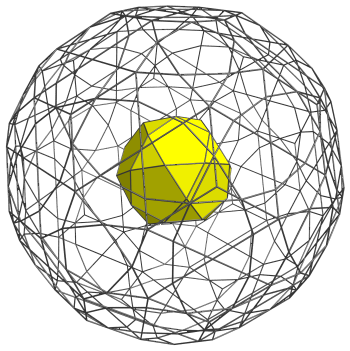
This icosidodecahedron may be considered to be the “north pole” cell. Its 20 triangular faces, shown here in red, are joined to the first layer of 20 tetrahedra that we have seen previously. Its 12 pentagonal faces are joined to the next layer of 12 icosidodecahedra, shown next:

The tetrahedral gaps visible here, and throughout the next several images, are filled in by the tetrahedral cells that we have seen previously. Straddling these 12 icosidodecahedra are another 20 icosidodecahedra, corresponding with the 20 vertices of a dodecahedron. These are shown next:

Next, another 12 icosidodecahedra fit where the green tetrahedra form rings of 5 each:

We have now reached the equator. There are 30 icosidodecahedra on the equator, corresponding with the edges of a dodecahedron. These are shown next:

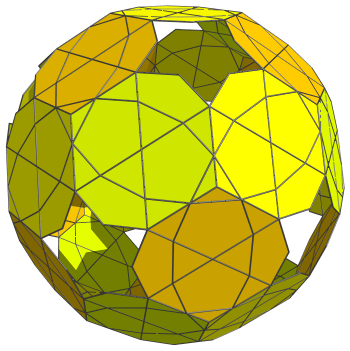
For clarity, we omit the cells that we have seen previously. These cells appear flat because they are seen at a 90° angle; they are perfectly uniform icosidodecahedra in 4D.

Past this point, we reach the southern hemisphere of the rectified 120-cell, which exactly corresponds with the layout of cells in the northern hemisphere with the layers in reverse order.

In summary, in the northern hemisphere there are 1+12+20+12=45 icosidodecahedra; on the equator are 30 icosidodecahedra; and in the southern hemisphere another 45 icosidodecahedra. Thus, this accounts for all 120 icosidodecahedra of the rectified 120-cell.

Perspective Projections

The following image shows the perspective projection of the rectified 120-cell's 120 icosidodecahedral cells.

[Full-size image]

We use the same coloring scheme as used in the previous section, but with increased transparency so that all layers of cells are visible. For clarity, only icosidodecahedra that lie on the near side of the rectified 120-cell are shown. The nearest icosidodecahedron to the 4D viewpoint is shown in yellow at the center of the image. Surrounding it are the 12 icosidodecahedra in the next layer, and in the outer layer are the 20+12 icosidodecahedra before we reach the equator. Due to foreshortening by the perspective projection, the equatorial cells lie on the far side of the rectified 120-cell, and are not visible here.

Coordinates

The Cartesian coordinates of the rectified 120-cell, centered on the origin and having edge length 2, are all permutations of coordinates and changes of sign of:

• (0, 0, 2φ, 2φ³)
• (0, 2φ², 2φ², 2φ²)
• (φ², φ², φ², 3φ²)
• (φ², φ², 1+3φ, 1+3φ)

together with even permutations of coordinates and all changes of sign of:

• (0, 1, φ⁴, 1+3φ)
• (0, φ, 3φ², φ³)
• (1, φ, 2φ³, φ²)
• (1, φ², φ⁴, 2φ²)
• (φ, φ³, 1+3φ, 2φ²)
• (φ², 2φ, φ⁴, φ³)

where φ=(1+√5)/2 is the Golden Ratio.