The Truncated 24-cell
The truncated 24-cell is a uniform polychoron bounded by 48 cells (24 cubes, 24 truncated octahedra), 240 polygons (144 squares, 96 hexagons), 384 edges, and 192 vertices. It is derived from the 24-cell by truncating its vertices to a depth of 1/3 its edge length.

The truncated 24-cell is actually the same as the cantitruncated 16-cell, due to the fact that the 24-cell is just the rectified 16-cell.
Structure
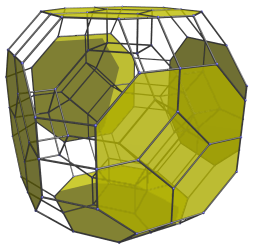
We will explore the truncated 24-cell by means of its parallel projection into 3D. The following image shows its cube-first projection, with all cells except the closest cube to the 4D viewpoint hidden.
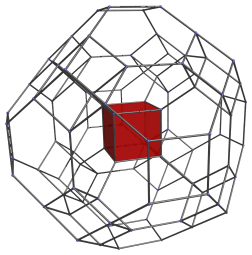
This projection has an envelope in the shape of a rhombic dodecahedron with its six axial vertices truncated. The central cube is joined to 6 truncated octahedra, shown in pairs below:
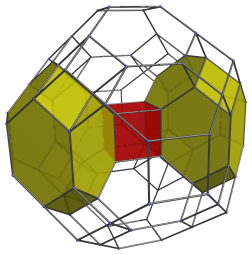
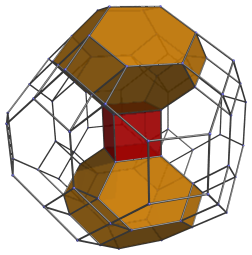

The next image shows all of them together:

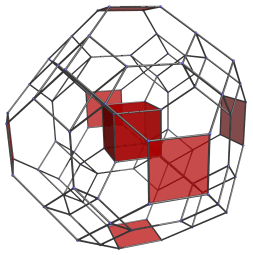
There are 8 obvious gaps into which 8 cubes may fit:

We have now reached the limb of the truncated 24-cell. The cells shown so far constitute the “northern hemisphere” cells, lying on the near half of the truncated 24-cell. At the “equator”, there are 6 cubes and 12 truncated octahedra, the former of which is shown below:
For reference, we also show the first cube in the center. The 6 cubes on the “equator” appear as flat squares, because they lie at a 90° angle to the 4D viewpoint.
The 12 truncated octahedra at the “equator” project to the hexagonal faces of the projection envelope:

These truncated octahedra appear as flat hexagons because they also lie at a 90° angle to the 4D viewpoint.
The cells on the far side of the truncated 24-cell (the “southern hemisphere”) have an arrangement that exactly mirrors the near side (the “northern hemisphere”). So in total, in the northern hemisphere we have 1+8=9 cubes, and 6 truncated octahedra. The southern hemisphere also has 9 cubes and 6 truncated octahedra, giving us 18 cubes and 12 truncated octahedra. Adding the equatorial cells, 6 cubes and 12 truncated octahedra, gives us 24 cubes and 24 truncated octahedra in total.
Perspective Projection
The following image shows the perspective projection of the truncated 24-cell:

It is almost the same as the previous parallel projection, except that the limb cells are hidden from view, and the projection envelope shows some foreshortening.
Cantitruncated 16-cell
The truncated 24-cell is the same as the cantitruncated 16-cell, because the 24-cell happens to be the same as the rectified 16-cell. The following parallel projections show the tesseractic symmetry of the truncated 24-cell, when viewed as the cantitruncated 16-cell:
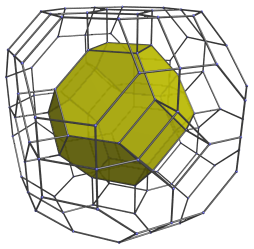
This projection is centered on a truncated octahedral cell. This nearest cell to the 4D viewpoint is shown above in yellow. Its square faces are joined to 6 cubical cells, as shown below:
These cubes appear slightly flattened, because they are seen at a 45° angle; in 4D, they are perfectly regular cubes.
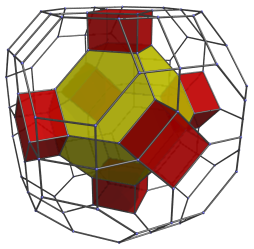
The hexagonal faces of the truncated octahedral cell are joined to 8 other truncated octahedra. We show them in 2 sets of 4 below:

Here they are all together:

These cells are, of course, perfectly uniform truncated octahedra; they appear a bit squished because they are seen at an angle.
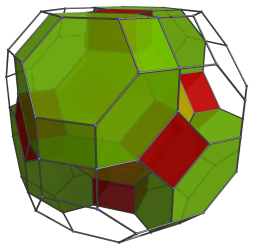
These are all the cells in the “Northern Hemisphere” of the cantitruncated 16-cell. Next, we have the equatorial cells, which consist of 6 more truncated octahedra:
And 12 cubes:

These truncated octahedra and cubes have been foreshortened into octagons and rectangles, because they are seen at a 90° angle. In 4D, they are perfectly uniform truncated octahedra and perfectly regular cubes.
Past this point, the cells repeat in reverse, forming the “Southern Hemisphere” of the cantitruncated 16-cell. In summary, we have 1+8=9 truncated octahedra in the northern hemisphere, 6 truncated octahedra on the equator, and another 9 truncated octahedra in the southern hemisphere, making a total of 24 truncated octahedra. There are 6 cubes in each hemisphere and 12 cubes on the equator, also totalling 24 cubes. Thus, we see that the truncated 24-cell and the cantitruncated 16-cell are one and the same.
Coordinates
The coordinates of the truncated 24-cell centered on the origin with an edge length of 2 are all permutations of coordinates and changes of sign of:
- (0, √2, 2√2, 3√2)
Properties
Since the 24-cell is self-dual, the 24 cubes and 24 truncated octahedra of the truncated 24-cell correspond with the cells and vertices of a 24-cell, or, equivalently, with the cells of a 24-cell and the cells of its dual, respectively. With the truncated 24-cell, these two sets of 24 cells have different shapes; the bitruncated 24-cell, on the other hand, has the same shape for both sets of cells, being bounded by 48 truncated cubes.




